In mathematics, a conic section (or just "conic") is a curve obtained from the intersection of a cone (more precisely, a right circular conical surface) with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2. There are a number of other geometric definitions possible, one of the most useful being that a conic consists of those points whose distances to some other point (called a focus) and some other line (called a directrix) are in a fixed ratio, called the eccentricity.
Traditionally, the three types of conic section are the hyperbola, the parabola, and the ellipse. The circle is a special case of the ellipse, and is of such interest in its own right that it is sometimes called the fourth type of conic section. The type of a conic corresponds to its eccentricity—those with eccentricity less than 1 being ellipses, those with eccentricity equal to 1 being parabolas, and those with eccentricity greater than 1 being hyperbolas. In the focus-directrix definition of a conic, the circle is a limiting case with eccentricity 0. In modern geometry, certain degenerate cases—such as the union of two lines—are included as conics as well.
In the Cartesian coordinate system, the graph of a quadratic equation in two variables is always a conic section—though it may be degenerate—and all conic sections arise in this way.
Conic sections are important in astronomy: the orbits of two massive objects that interact according to Newton's law of universal gravitation are conic sections if their common center of mass is considered to be at rest. If they are bound together, they will both trace out ellipses; if they are moving apart, they will both follow parabolas or hyperbolas. In projective geometry, the conic sections in the projective plane are equivalent to each other up to projective transformations.
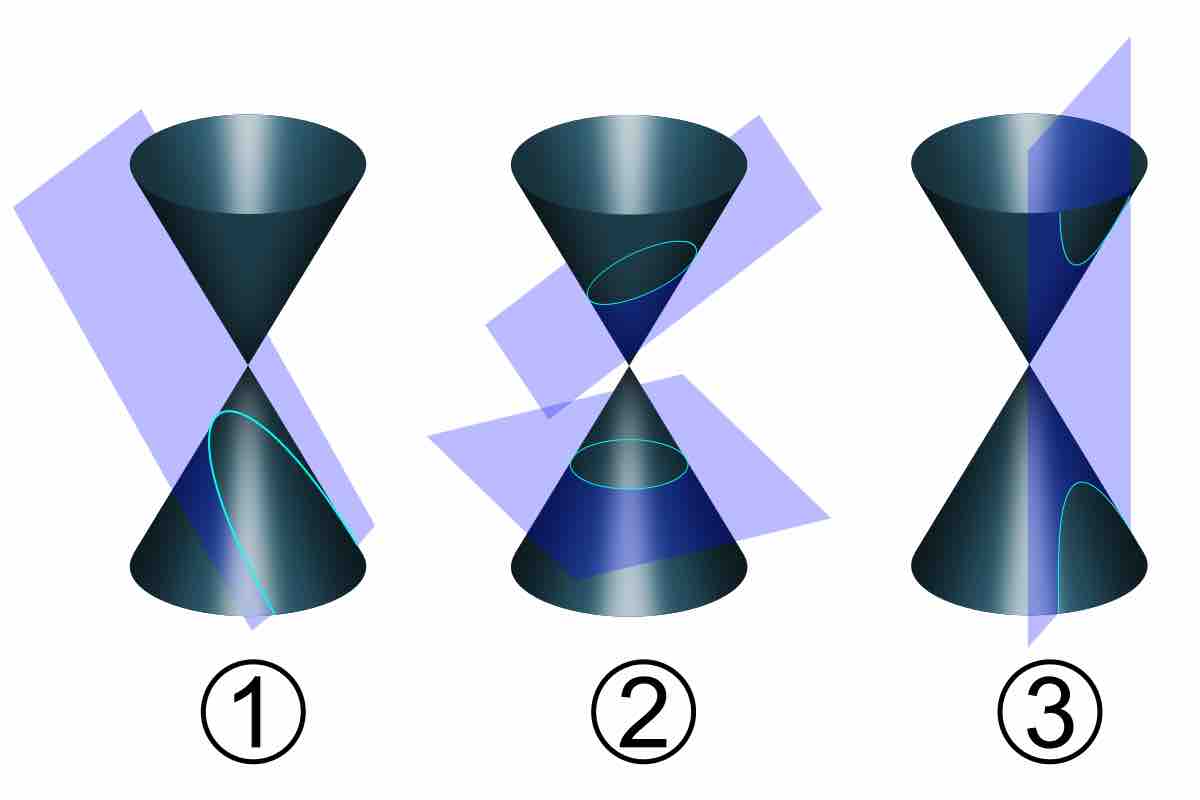
Types of Conic Sections
There are three types of conic sections: 1.Parabola; 2. Ellipse; 3. Hyperbola.