Arc Length and Speed

The length of a curve can be difficult to measure. A curve may be thought of as an infinite number of infinitesimal straight line segments, each pointing in a slightly different direction to make up the curve. Adding up all these lengths together would be equivalent to stretching the curve out straight and measuring its length. The length of the curve is called the arc length.

In order to calculate the arc length, we use integration because it is an efficient way to add up a series of infinitesimal lengths.

Arc lengths can be used to find the distance traveled by an object with an arcing path. Consider a case in which an object movies along a path in the Cartesian plane (the $xy$-plane). Its position horizontally is given by $x=f(t)$ and its position vertically is given by $y=g(t)$, where $f$ and $g$ are functions which depend on a parameter, $t$. Since there are two functions for position, and they both depend on a single parameter—time—we call these equations parametric equations.

The distance, or arc length, the object travels through its motion is given by the equation:

$\displaystyle{D = \int_{t_1}^{t_2} \sqrt{ \left(\frac{dx}{dt} \right)^2 + \left(\frac{dy}{dt} \right)^2} dt}$

This equation is obtained using the Pythagorean Theorem. The arc length is calculated by laying out an infinite number of infinitesimal right triangles along the curve. Each of these triangles has a width $dx$ and a height $dy$, standing for an infinitesimal increase in $x$ and $y$. By the Pythagorean Theorem, each hypotenuse will have length $\sqrt{dx^2 + dy^2}$. Adding up each tiny hypotenuse yields the arc length.

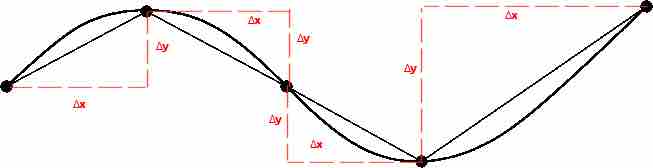
Approximating Arc Length with Hypotenuses

The length of a curve can be approximated by using a series of right triangles with the hypotenuses lying along the curve. The smaller the triangles one uses, the closer the approximation will be.

However, since $x$ and $y$ depend on the parameter $t$, we will want to integrate over $t$, not over $x$ and $y$. Taking the derivative of $x$ and $y$ with respect to $t$, we find the rate of change of the distance with time. This is also known as the speed. As shown previously using the Pythagorean Theorem, it is given by:

$\displaystyle{\sqrt{ \left(\frac{dx}{dt} \right)^2 + \left(\frac{dy}{dt} \right)^2}}$

where the rate of change of the hypotenuse length depends on the rate of change of $x$ and $y$. Integrating the speed with respect to time gives the distance as shown above.