Arc Length
If you were to straighten a curved line out, the measured length would be the arc length. Since it can be very difficult to measure the length of an arc linearly, the solution is to use polar coordinates. Using polar coordinates allows us to integrate along the length of the arc in order to compute its length.
The arc length of the curve defined by a polar function is found by the integration over the curve
Solving this integral will give the length of the arc.
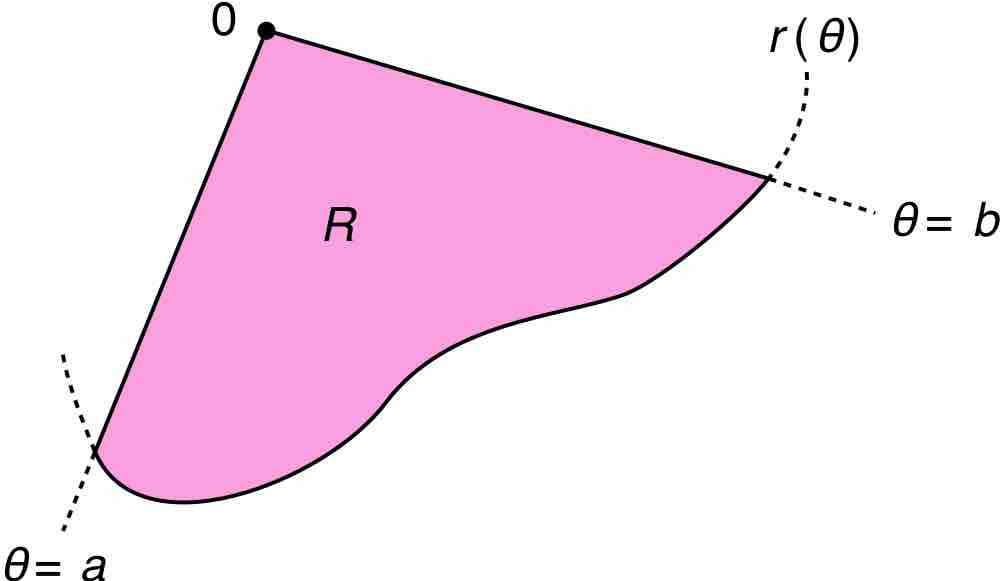
Arc Length
The curved lines bounding the region
Arc Segment Area
To find the area enclosed by the arcs and the radius and polar angles, you again use integration.
Let
This result can be found as follows.
First, the interval
And the total area is the sum of these sectors. An infinite sum of these sectors is the same as integration.