We use coordinate systems every day, even if we don't realize it. For example, if you walk 20 meters to the right of the parking lot to find the car, you are using a coordinate system. Coordinate systems are a way of determining the location of a point or object of interest in relation to something else. The coordinate system you are most likely familiar with is the
The
In polar coordinates, each point on a plane is defined by a distance from a fixed point and an angle from a fixed direction.
The distance is known as the radial distance and is usually denoted as
The angle is known as the polar angle, or radial angle, and is usually given as
A positive angle is usually measured counterclockwise from the polar axis, and a positive radius is in the same direction as the angle. A negative radius would be opposite the direction of the angle and a negative angle would be measured clockwise from the polar axis. The polar axis is usually drawn horizontal and pointing to the right .
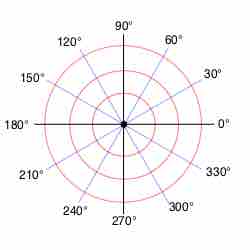
Polar Coordinates
A set of polar coordinates. Note the polar angle increases as you go counterclockwise around the circle with 0 degrees pointing horizontally to the right.
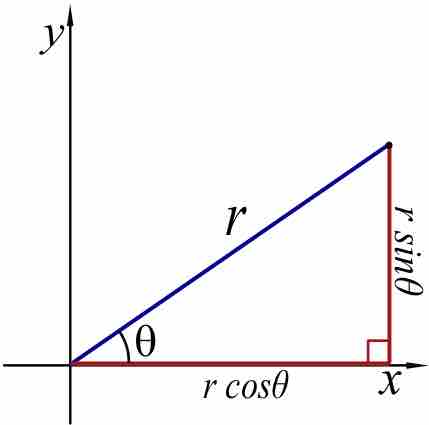
Relation between Cartesian and Polar Coordinates
The
Polar coordinates in