The predator–prey equations are a pair of first-order, non-linear, differential equations frequently used to describe the dynamics of biological systems in which two species interact, one a predator and one its prey.
They evolve in time according to the pair of equations:
where
The model makes a number of assumptions about the environment and evolution of the predator and prey populations:
- The prey population finds ample food at all times.
- The food supply of the predator population depends entirely on the prey populations.
- The rate of change of population is proportional to its size.
- During the process, the environment does not change in favor of one species and the genetic adaptation is sufficiently slow.
- As differential equations are used, the solution is deterministic and continuous. This, in turn, implies that the generations of both the predator and prey are continually overlapping.
The prey are assumed to have an unlimited food supply, and to reproduce exponentially unless subject to predation; this exponential growth is represented in the equation above by the term
In the predator equation,
The equations have periodic solutions and do not have a simple expression in terms of the usual trigonometric functions. They can only be solved numerically. However, a linearization of the equations yields a solution similar to simple harmonic motion with the population of predators following that of prey by 90 degrees.
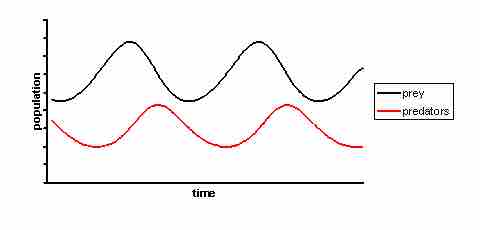
Solution to the equation
The solutions to the equations are periodic. The predator population follows the prey population.