Parametric Equations

In mathematics, a parametric equation of a curve is a representation of the curve through equations expressing the coordinates of the points of the curve as functions of a variable called a parameter. For example,

$x = \cos(t) \\ y = \sin(t)$

is a parametric equation for the unit circle, where $t$ is the parameter. A common example occurs in kinematics, where the trajectory of a point is usually represented by a parametric equation with time as the parameter. The notion of parametric equation has been generalized to surfaces of higher dimension with a number of parameters equal to the dimension of the manifold (dimension one and one parameter for curves, dimension two and two parameters for surfaces, etc.)

For example, the simplest equation for a parabola $y=x^2$ can be parametrized by using a free parameter $t$, and setting $x=t$ and $y = t^2$.

This way of expressing curves is practical as well as efficient; for example, one can integrate and differentiate such curves term-wise. Thus, one can describe the velocity of a particle following such a parametrized path as follows:

$v(t) = (x'(t), y'(t))$

This is a function of the derivatives of $x$ and $y$ with respect to the parameter $t$.

Converting a set of parametric equations to a single equation involves eliminating the variable from the simultaneous equations. If one of these equations can be solved for $t$, the expression obtained can be substituted into the other equation to obtain an equation involving $x$ and $y$ only. If there are rational functions, then the techniques of the theory of equations such as resultants can be used to eliminate $t$. In some cases there is no single equation in closed form that is equivalent to the parametric equations.

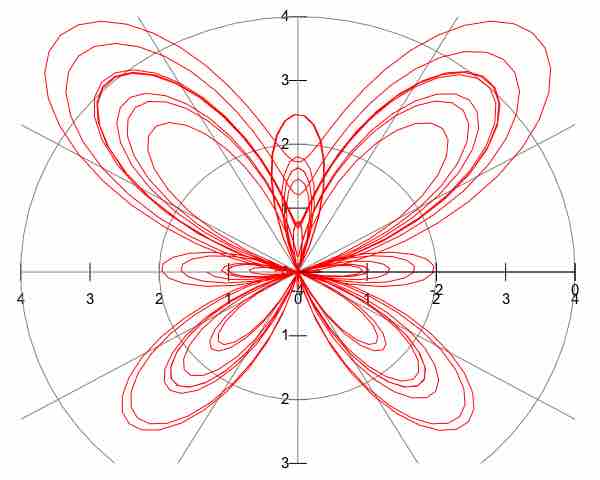
Parametric Example

One example of a sketch defined by parametric equations. Note that it is graphed on parametric axes.