A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable.
A common form of a linear equation in the two variables
where
Since terms of linear equations cannot contain products of distinct or equal variables, nor any power (other than
Linear equations can be written in parametric form:
The parametric form of a linear equation involves two simultaneous equations in terms of a variable parameter
- slope (
$m$ ):$\displaystyle{\frac{V }{ T}}$ - x-intercept:
$\displaystyle{\frac{VU−WT}{V}}$ - y-intercept:
$\displaystyle{\frac{ WT−VU}{ T}}$
Linear differential equations are differential equations that have solutions which can be added together to form other solutions. They can be ordinary or partial. Linear differential equations are of the form:
where the differential operator
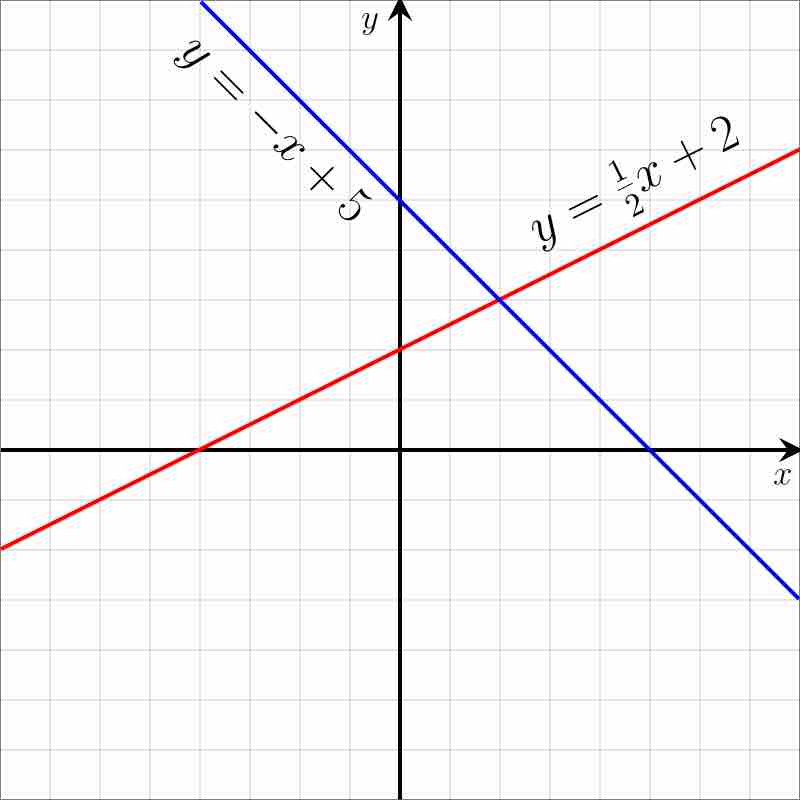
Linear equations
Graphical example of linear equations.