Logistic Equations and Population Grown

The logistic function is the solution of the following simple first-order non-linear differential equation:

$\displaystyle{\frac{d}{dt}P(t)=P(t)(1-P(t))}$

with boundary condition $P(0) = \frac{1}{2}$.

The derivative is $0$ at $P = 0$ or $P = 1$, and the derivative is positive for $0 \leq P \leq 1$ and negative for $1 < P$ or $P < 0$ (though negative populations do not generally accord with a physical model). This yields an unstable equilibrium at $0$ and a stable equilibrium at $1$, and thus for $0 < P < 1$ , $P$ grows to $1$. One may readily find the (symbolic) solution to be as follows:

$\displaystyle{P(t)=\frac{e^t}{e^t+e^c}}$

Choosing the constant of integration $e^c = 1$ gives the other well-known form of the definition of the logistic curve:

$\displaystyle{P(t)=\frac{e^t}{e^t +1}}$

More quantitatively, as can be seen from the analytical solution, the logistic curve shows early exponential growth for negative $t$, which slows to linear growth of slope $\frac{1}{4}$ near $t = 0$, then approaches $y = 1$ with an exponentially decaying gap.

The logistic equation is commonly applied as a model of population growth, where the rate of reproduction is proportional to both the existing population and the amount of available resources, all else being equal. The equation describes the self-limiting growth of a biological population.

Letting $P$ represent population size ($N$ is often used instead in ecology) and $t$ represent time, this model is formalized by the following differential equation:

$\displaystyle{\frac{dP}{dt}=rP \left( 1-\frac{P}{K} \right)}$

where the constant $r$ defines the growth rate and $K$ is the carrying capacity. In the equation, the early, unimpeded growth rate is modeled by the first term $rP$. The value of the rate $r$ represents the proportional increase of the population $P$ in one unit of time. Later, as the population grows, the second term, which multiplied out is $\frac{−rP^2}{K}$, becomes larger than the first as some members of the population $P$ interfere with each other by competing for some critical resource, such as food or living space. This antagonistic effect is called the bottleneck, and is modeled by the value of the parameter $K$. The competition diminishes the combined growth rate, until the value of $P$ ceases to grow (this is called maturity of the population).

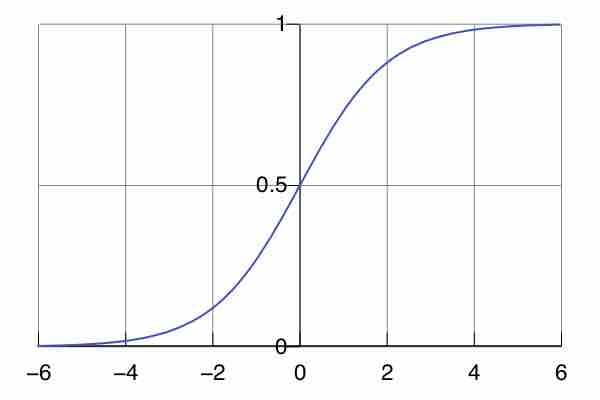
Logistic Curve

The standard logistic curve. It can be used to model population growth because of the limiting effect scarcity has on the growth rate. This is represented by the ceiling past which the function ceases to grow.