Work

For moving objects, the rate of the work done by a force (measured in joules/second, or watts) is the scalar product of the force (a vector) and the velocity vector of the point of application. This scalar product of force and velocity is classified as instantaneous power delivered by the force. Just as velocities may be integrated over time to obtain a total distance, by the fundamental theorem of calculus, the total work along a path is similarly the time-integral of instantaneous power applied along the trajectory of the point of application.

Work is the result of a force on a point that moves through a distance. As the point moves, it follows a curve $X$, with a velocity $v$, at each instant. The small amount of work $\delta W$ that occurs over an instant of time $\delta t$ is calculated as:

 $\delta W = \mathbf{F}\cdot\mathbf{v}\delta t$

where the term $\mathbf{F}\cdot\mathbf{v}$ is the power over the instant $\delta t$. The sum of these small amounts of work over the trajectory of the point yields the work:

$\displaystyle{W = \int_{t_1}^{t_2}\mathbf{F} \cdot \mathbf{v}dt}$

$\displaystyle{\quad = \int_{t_1}^{t_2}\mathbf{F} \cdot {\frac{d\mathbf{x}}{dt}}dt}$

$\displaystyle{\quad =\int_C \mathbf{F} \cdot d\mathbf{x}}$

where $C$ is the trajectory from $x(t_1)$ to $x(t_2)$. This integral is computed along the trajectory of the particle, and is therefore said to be path-dependent. If the force is always directed along this line, and the magnitude of the force is $F$, then this integral simplifies to:

$\displaystyle{W=\int_C \mathbf{F} \, ds}$

where $s$ is distance along the line. If $F$ is constant, in addition to being directed along the line, then the integral simplifies further to:

 $\displaystyle{W = \int_C Fds = F\int_C ds = Fd}$

This calculation can be generalized for a constant force that is not directed along the line, followed by the particle. In this case the dot product $F·dx = F \cdot \cos \theta \cdot dx$ , where $\theta$ is the angle between the force vector and the direction of movement. This is to say:

 $\displaystyle{W = \int_C \mathbf{F} \cdot d\mathbf{x} = Fd\cos\theta}$

Example: Work Done by a Spring

Let's consider an object with mass $m$ attached to an ideal spring with spring constant $k$. When the object moves from $x=x_0$ to $x=0$, work done by the spring would be:

 $\displaystyle{W = \int_C \mathbf{F_s} \cdot d\mathbf{x} = \int_{x_0}^{0} (-kx)dx = \frac{1}{2} k x_0^2}$

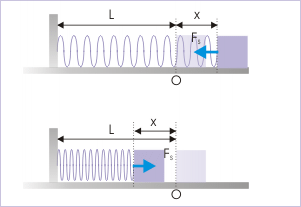
Spring and Restoring Force

The spring applies a restoring force ($-k \cdot x$) on the object located at $x$. Work done by the restoring force leads to increase in the kinetic energy of the object.