Newton's Method

In numerical analysis, Newton's method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function. In other words find $x$ such that $f(x)=0$. Also known as the $x$-intercept.

The Newton-Raphson method in one variable is implemented as follows:

1. Given a function ƒ defined over the reals x, and its derivative ƒ ', we begin with a first guess x₀ for a root of the function f. Provided the function satisfies all the assumptions made in the derivation of the formula, a better approximation x₁ is x₀ - f(x₀) / f'(x₀). Geometrically, (x₁, 0) is the intersection with the x-axis of a line tangent to f at (x₀, f (x₀)).The process is repeated as x_n+1 = x_n - f(x_n / f'(x_n) until a sufficiently accurate value is reached.

This algorithm is first in the class of Householder's methods, succeeded by Halley's method. The method can also be extended to complex functions and to systems of equations.

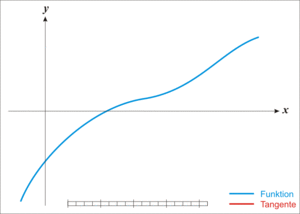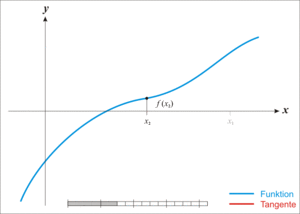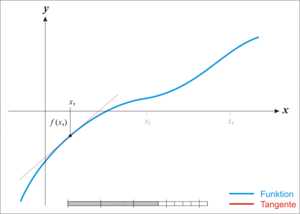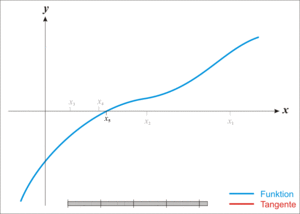
Newton's Method

The function $f$ is shown in blue and the tangent line in red. We see that $x_{n+1}$ is a better approximation than $x_n$ for the root $x$ of the function $f$.

The idea of the method is as follows: one starts with an initial guess which is reasonably close to the true root, then the function is approximated by its tangent line (which can be computed using the tools of calculus), and one computes the $x$-intercept of this tangent line (which is easily done with elementary algebra). This $x$-intercept will typically be a better approximation to the function's root than the original guess, and the method can be iterated.