Inverse function is a function that undoes another function: If an input
A function
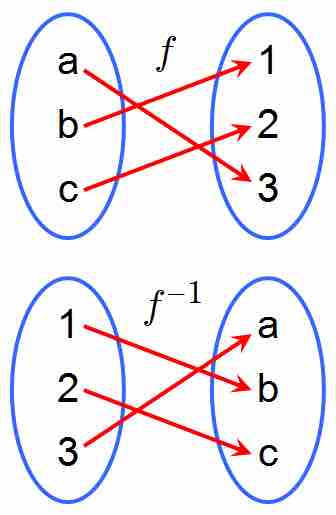
A Function and its Inverse
A function
Examples
Inverse operations that lead to inverse functions
Inverse operations are the opposite of direct variation functions. Direct variation function are based on multiplication;
Squaring and square root functions
The function