Exponential Function
Exponential function is the function
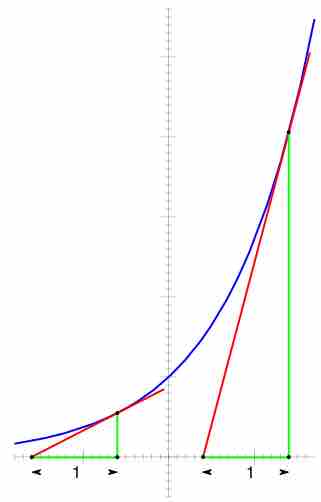
Graph of $f(x)=e^x$
The derivative (or slope of a tangential line) of the exponential function is equal to the value of the function.
The exponential function arises whenever a quantity grows or decays at a rate proportional to its current value. One such situation is continuously compounded interest, and in fact it was this that led Jacob Bernoulli in 1683 to the number
The exponential function
Logarithmic Functions
The logarithm of a number
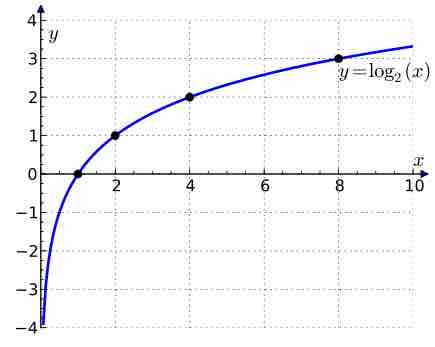
Plot of $\log_2(x)$
The graph of the logarithm to base 2 crosses the x-axis (horizontal axis) at 1 and passes through the points with coordinates
For