Tangent and Velocity Problems

Calculus has widely used in physics and engineering. In this atom, we will learn that instantaneous velocity can be obtained from a position-time curve of a moving object by calculating derivatives of the curve.

Velocity is defined as rate of change of displacement. The average velocity $\bar{\vec{v}}$ of an object moving through a displacement ($\Delta \vec{x}$) during a time interval ($\Delta t$) is described by the formula: $\displaystyle \bar{\vec{v}} = \frac{\Delta \vec{x}}{\Delta t}$.

What will happen when we reduce the time interval Δt\Delta t and let it approach 0? The average velocity becomes instantaneous velocity at time t. Suppose an object is at positions $\vec{x}(t)$ at time $t$ and $\vec{x}(t+\Delta t)$ time $t + \Delta t$. The velocity $\vec{v}$ of the object can be computed as the derivative of position: $\displaystyle \vec{v} = \lim\limits_{\Delta t \to 0}{{\vec{x}(t+\Delta t)-\vec{x}(t)} \over \Delta t}={\mathrm{d} \vec{x} \over \mathrm{d}t}$ . Instantaneous velocity is always tangential to trajectory. Slope of tangent of position or displacement time graph is instantaneous velocity and its slope of chord is average velocity.

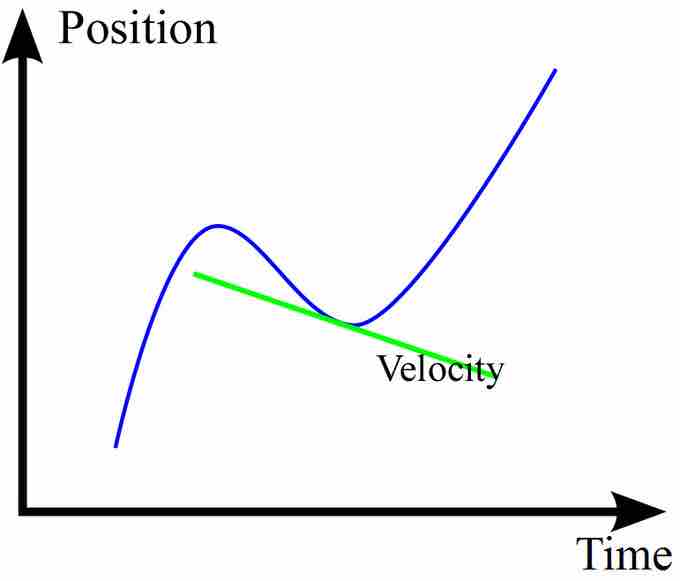
Instantaneous Velocity

The green line shows the tangential line of the position-time curve at a particular time. Its slope is the velocity at that point.

On the other hand, the equation for an object's position can be obtained mathematically by evaluating the definite integral of the equation for its velocity beginning from some initial period time $t_0$ to some point in time later $t_n$. That is $x(t) = x_0 + \int_{t_0}^{t} v(t')~dt'$, where $x_0$ is the position of the object at $t=t_0$. For the simple case of constant velocity, the equation gives $x(t)-x_0 = v_0 (t-t_0)$.