Limit of a Function

The limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input. Informally, a function $f$ assigns an output $f(x)$ to every input $x$. The function has a limit $L$ at an input $p$ if $f(x)$ is "close" to $L$ whenever $x$ is "close" to $p$. In other words, $f(x)$ becomes closer and closer to $L$ as $x$ moves closer and closer to $p$. More specifically, when $f$ is applied to each input sufficiently close to $p$, the result is an output value that is arbitrarily close to $L$. If the inputs "close" to $p$ are taken to values that are very different, the limit is said to not exist.

The notion of a limit has many applications in modern calculus. In particular, the many definitions of continuity employ the limit: roughly, a function is continuous if all of its limits agree with the values of the function. It also appears in the definition of the derivative: in the calculus of one variable, this is the limiting value of the slope of secant lines to the graph of a function.

To say that $\displaystyle \lim_{x \to p}f(x) = L$ means that $f(x)$ can be made as close as desired to $L$ by making $x$ close enough, but not equal, to $p$.

Alternatively, $x$ may approach $p$ from above (right) or below (left), in which case the limits may be written as $\displaystyle \lim_{x \to p^+}f(x) = L_+$ or $\displaystyle \lim_{x \to p^-}f(x) = L_-$. If both of these limits are equal to $L$ then this can be referred to as the limit of $f(x)$ at $p$. Conversely, if they are not both equal to $L$ then the limit, as such, does not exist. In the following atoms, we will learn about more strict and precise definition of the limit of a function.

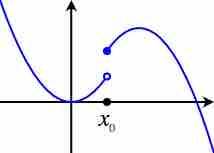
Nonexistence of Limit

The limit as the function approaches $x_0$ from the left does not equal the limit as the function approaches $x_0$ from the right, so the limit of the function at $x_0$ does not exist. 

Example: A function without a limit as seen in : $f(x)=\begin{cases}\sin\frac{5}{x-1} & \mbox{ for } x< 1 \\ 0 & \mbox { for } x=1 \\ \frac{0.1}{x-1}& \mbox{ for } x>1\end{cases}$ has has no limit at $x_0 = 1$.

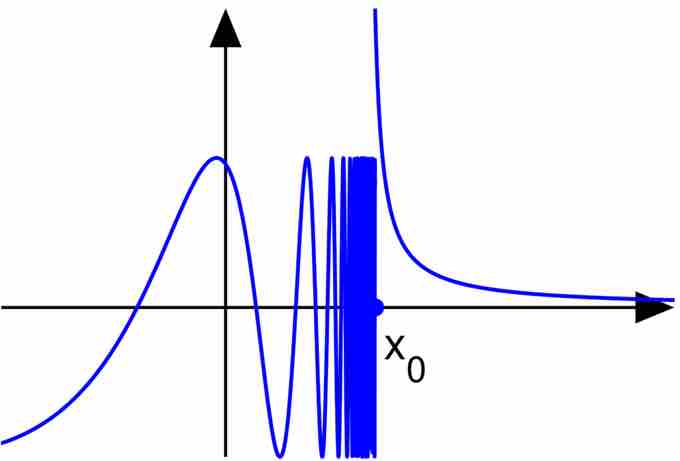
Essential Discontinuity

A graph of the above function, demonstrating that the limit at $x_0$ does not exist.