The inverse of an exponential function is a logarithmic function and vice versa. That is, the two functions undo each other. Thus
Another way of saying this is that if
Lastly, as with all inverse functions, if we graph
In the following graph you can see an exponential function in red and its inverse, a logarithmic function, in blue. The graphs are symmetric over the line
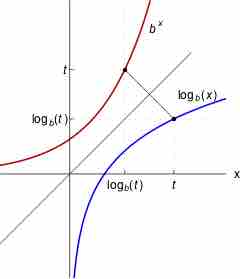
Logarithm function
The graph of the logarithm function
Thus far we have been looking at logs of the base
As they are inverses composing these two functions in either order yields the original input. That is,