Composition and Composite Functions
In mathematics, function composition is the application of one function to the results of another.
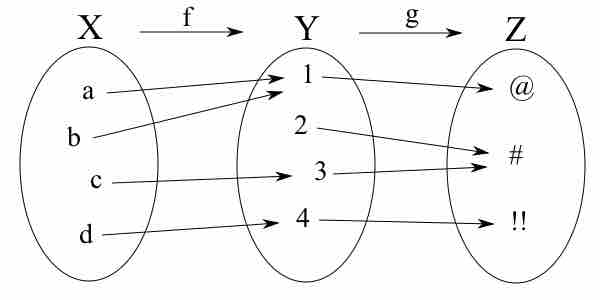
Composition of functions
g ∘ f, the composition of f and g. For example, (g ∘ f)(c) = #.
The functions
A composite function represents in one function the results of an entire chain of dependent functions. For example, if a school becomes larger, the supply of food in the cafeteria must become larger. This would entail ordering more sandwiches, which means ordering more ingredients, drinks, plates, etc. The entire chain of dependent functions are the ingredients, drinks, plates, etc., and the one composite function would be putting the entire chain together in order to calculate a larger population at the school.
Inverses and Composition
If
This statement is equivalent to the first of the above-given definitions of the inverse, and it becomes equivalent to the second definition if
Example 1
Let's go through the relationship between inverses and composition in this example. let's take two functions, compose and invert them.
Find: