Inverse Functions
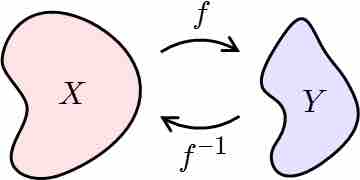
Inverse functions' domain and range
If
Domain Restrictions: Parabola
Informally, a restriction of a function is the result of trimming its domain.
Remember that:
If
Without any domain restriction,
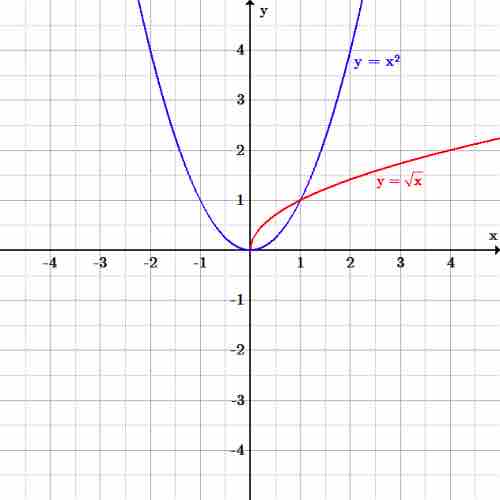
Failure of horizontal line test
Graph of a parabola with the equation
Domain Restriction: Exponential and Logarithmic Functions
Domain restriction is important for inverse functions of exponents and logarithms because sometimes we need to find an unique inverse. The inverse of an exponential function is a logarithmic function, and the inverse of a logarithmic function is an exponential function.
Example 1
Is
No, the function has no defined value for