Systems of Equations in Three Variables
In mathematics, simultaneous equations are a set of equations containing multiple variables. This set is often referred to as a system of equations. A solution to a system of equations is a particular specification of the values of all variables that simultaneously satisfies all of the equations. Graphically, the solution is where the functions intersect.
In a system of equations in three variables, you can have one or more equations, each of which may contain one or more of the three variables, usually x, y, and z. The introduction of the variable z means that the graphed functions now represent planes, rather than lines.
A Simple Example
This is a set of linear equations, also known as a linear system of equations, in three variables:
The solution to this system of equations is:
Plug in these values to each of the equations to see that the solution satisfies all three of the equations.
Solving Systems of Equations in Three Variables
Graphical Method
The graphical method of solving a system of equations in three variables involves plotting the planes that are formed when graphing each equation in the system and then finding the intersection point of all three planes. The single point where all three planes intersect is the unique solution to the system.
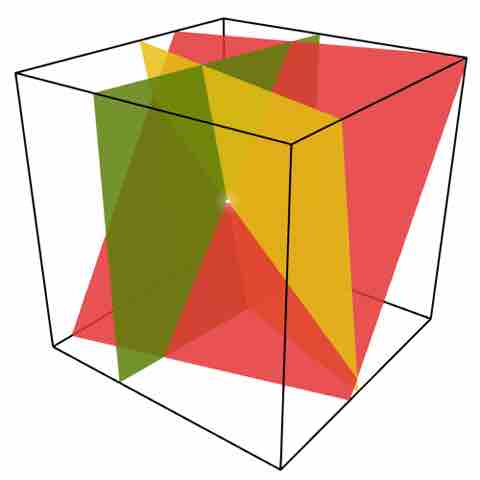
System of linear equations
This images shows a system of three equations in three variables. The intersecting point (white dot) is the unique solution to this system.
Substitution Method
The substitution method of solving a system of equations in three variables involves identifying an equation that can be easily by written with a single variable as the subject (by solving the equation for that variable). Next, substitute that expression where that variable appears in the other two equations, thereby obtaining a smaller system with fewer variables. After that smaller system has been solved, whether by further application of the substitution method or by other methods, substitute the solutions found for the variables back into the first right-hand side expression.
For example, consider this system of equations:
Since the coefficient of z is already 1 in the first equation, solve for z to get:
Substitute this expression for z into the other two equations:
This new system simplifies to:
Now solving for x in the first equation, one gets:
Substitute this expression for x into the last equation in the system and solve for y:
Now that you have the value of y, work back up the equation. Plug
Working up again, plug
Therefore, the solution to the system of equations is
Elimination Method
Elimination by judicious multiplication is the other commonly-used method to solve simultaneous linear equations. It uses the general principles that each side of an equation still equals the other when both sides are multiplied (or divided) by the same quantity, or when the same quantity is added (or subtracted) from both sides.
As the equations grow simpler through the elimination of some variables, a variable will eventually appear in fully solvable form, and this value can then be "back-substituted" into previously derived equations by plugging this value in for the variable. Typically, each "back-substitution" can then allow another variable in the system to be solved.
Let's look at the following system:
Using the elimination method, begin by subtracting the first equation from the second and simplifying:
We now have the following system of equations:
Now subtract two times the first equation from the third equation to get
Doing this shows the new system:
Next, subtract two times the third equation from the second equation and simplify:
Doing this shows the new system:
Finally, subtract the third and second equation from the first equation to get
The final, solved system, therefore, is: