Higher degree polynomial equations can be very difficult to solve. In some special situations, however, they can be made more manageable by reducing their exponents via substitution. If a substitution can be made such that the higher order polynomial takes the form of a quadratic, any method for solving a quadratic equation can be applied.
For example, if a quartic equation is biquadratic—that is, it includes no terms of an odd-degree— there is a quick way to find the zeroes of the quartic function by reducing it into a quadratic form. Consider a quadratic function with no odd-degree terms which has the form:
If we let an arbitrary variable
With substitution, we were able to reduce a higher order polynomial into a quadratic equation. It can now be solved with any of a number of methods (via graphing, factoring, completing the square, or by using the quadratic formula).
Once values of
As with every square root, the root of
Example
As an example, consider the equation:
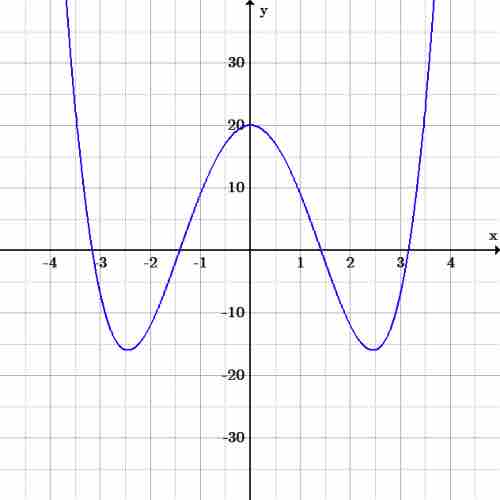
Quartic graph
Graph of the function
We can substitute the arbitrary variable
This equation is now solvable for
Simplifying this, we find
Knowing that
A similar procedure can be used to solve higher-order equations. The requirement is that there are two terms of