Recall that a quadratic function has the form
where
The graph of a quadratic function is a U-shaped curve called a parabola. This shape is shown below.
Parabola
The graph of a quadratic function is a parabola.
In graphs of quadratic functions, the sign on the coefficient
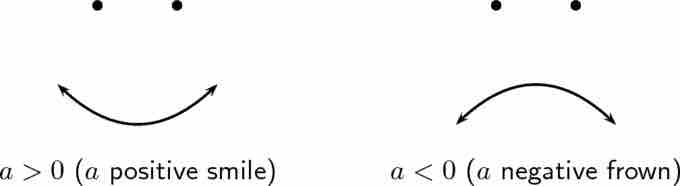
Direction of Parabolas
The sign on the coefficient
Features of Parabolas
Parabolas have several recognizable features that characterize their shape and placement on the Cartesian plane.
Vertex
One important feature of the parabola is that it has an extreme point, called the vertex. If the parabola opens up, the vertex represents the lowest point on the graph, or the minimum value of the quadratic function. If the parabola opens down, the vertex represents the highest point on the graph, or the maximum value. In either case, the vertex is a turning point on the graph.
Axis of Symmetry
Parabolas also have an axis of symmetry, which is parallel to the y-axis. The axis of symmetry is a vertical line drawn through the vertex.
$y$ -intercept
The y-intercept is the point at which the parabola crosses the y-axis. There cannot be more than one such point, for the graph of a quadratic function. If there were, the curve would not be a function, as there would be two
$x$ -intercepts
The x-intercepts are the points at which the parabola crosses the x-axis. If they exist, the x-intercepts represent the zeros, or roots, of the quadratic function, the values of
Possible $x$ -intercepts
A parabola can have no x-intercepts, one x-intercept, or two x-intercepts.
Recall that if the quadratic function is set equal to zero, then the result is a quadratic equation. The solutions to the equation are called the roots of the function. These are the same roots that are observable as the
Notice that, for parabolas with two