Recall how the roots of quadratic functions can be found algebraically, using the quadratic formula
Consider the quadratic function that is graphed below. Let's solve for its roots both graphically and algebraically.
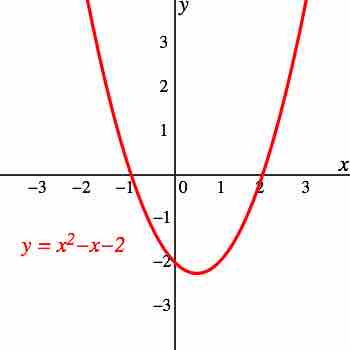
Graph of the quadratic function $f(x) = x^2 - x - 2$
Graph showing the parabola on the Cartesian plane, including the points where it crosses the x-axis.
Notice that the parabola intersects the
Now, let's solve for the roots of
Recall that the quadratic equation sets the quadratic expression equal to zero instead of
Now the quadratic formula can be applied to find the
Substitute these values in the quadratic formula:
Simplifying, we have:
and
We now have two possible values for x:
These reduce to
Example
Find the roots of the quadratic function
The graph of $f(x) = x^2 - 4x + 4$ .
The graph of the above function, with the vertex labeled at
Looking at the graph of the function, we notice that it does not intersect the
We can verify this algebraically. First, identify the values for the coefficients:
Substituting these into the quadratic formula, we have:
Simplifying, we have:
Notice that we have