Linear Inequalities
When two linear expressions are not equal, but are designated as less than (
For inequalities that contain variable expressions, you may be asked to solve the inequality for that variable. This just means that you need to find the values of the variable that make the inequality true.
A linear inequality looks like a linear equation, with the inequality sign replacing the equal sign. The same properties for solving an equation are used to solve an inequality; however, when solving an equation there is one solution (or one value that makes the equation true), but when solving an inequality there are many solutions (or values that make the statement true).
Solutions of Linear Inequalities
Example: Graph the solutions of the inequality: $x>4$
The solutions to this inequality includes every number that is greater than
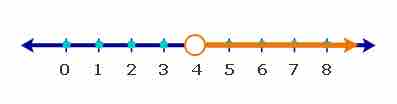
Inequality
Solutions to
Solving Linear Inequalities
Solving the inequality is the same as solving an equation. There is only one rule that is different: When you multiply or divide each side of an inequality by a negative number, you must reverse the inequality symbol to maintain a true statement.
Example: Solve the inequality: $-7x+3+x \leq 1-4x-10$
Step 1, combine like terms on each side of the inequality symbol:
Step 2, since there is a variable on both sides of the inequality, choose to move the
Adding
Step 3, this is similar to solving a two step equation. Subtract
Finally, divide both sides by
To read this answer, read from right to left,