Parallel Lines

Two lines in a plane that do not intersect or touch at a point are called parallel lines. The parallel symbol is $\parallel$. 

For example, given two lines: $f(x)=m_{1}x+b_{1}$and $g(x)=m_{2}x+b_{2}$, writing $f(x)$ $\parallel$ $g(x)$ states that the two lines are parallel to each other.  In 2D, two lines are parallel if they have the same slope. 

Given two parallel lines $f(x)$ and $g(x)$, the following is true:

1. Every point on $f(x)$ is located at exactly the same minimum distance from $g(x)$.
2. Line $f(x)$ is on the same plane as $g(x)$ but does not intersect $g(x)$, even assuming that the two lines extend to infinity in either direction.

Recall that the slope-intercept form of an equation is: $y=mx+b$ and the point-slope form of an equation is: $y-y_{1}=m(x-x_{1})$, both contain information about the slope, namely the constant $m$. If two lines, say $f(x)=mx+b$ and $g(x)=nx+c$, are parallel, then $n$ must equal $m$.

For example, in the graph below, $f(x)=2x+3$ and $g(x)=2x-1$ are parallel since they have the same slope, $m=2$.

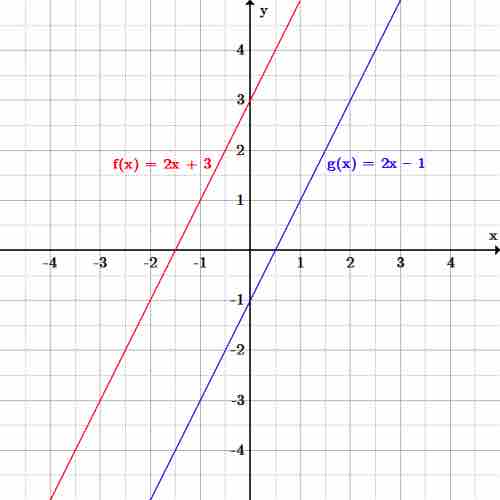
Parallel lines

$f(x)=2x+3$ in red is parallel to $g(x)=2x-1$ in blue; the slopes obtained from the graphs of the lines is the same as the slopes in their equations.

Perpendicular Lines

Two lines are perpendicular to each other if they form congruent adjacent angles. In other words, they are perpendicular if the angles at their intersection are right angles, $90$ degrees . The perpendicular symbol is $\perp$. 

For example given two lines, $f(x)=m_{1}x+b_{1}$ and $g(x)=m_{2}x+b_{2}$, writing$f(x)\perp g(x)$ states that the two lines are perpendicular to each other.

For two lines in a 2D plane to be perpendicular, their slopes must be negative reciprocals of one another, or the product of their slopes must equal $-1$.  This means that if the slope of one line is $m$, then the slope of its perpendicular line is $\frac{-1}{m}$. The two slopes multiplied together must equal $-1$. However, this method cannot be used if the slope is zero or undefined (the line is parallel to an axis).  

Given two lines: $f(x)=3x-2$ and $g(x)=\frac{-1}{3}x+1$, note the values of the slopes.  Since $3$ is the negative reciprocal of $-\frac{1}{3}$, the two lines are perpendicular. Also, the product of the slopes equals $-1$. 

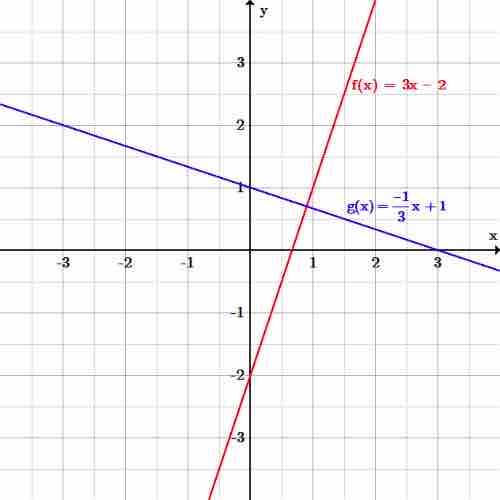
Perpendicular lines

The line $f(x)=3x-2$ in red is perpendicular to line $g(x)=\frac{-1}{3}x+1$ in blue. The values of their slopes are negative reciprocals of each other; therefore, the angle of intersection is $90$ degrees.

Writing Equations of Parallel and Perpendicular Lines

Example:  Write an equation of the line (in slope-intercept form) that is parallel to the line $y=-2x+4$ and passes through the point $(-1,1)$  

Start with the equation for slope-intercept form and then substitute the values for the slope and the point, and solve for $b$: $y=mx+b$.  The value of the slope will be equal to the current line, since the new line is parallel to it.  The point $(-1,1)$ is substituted for $(x,y)$.

$\displaystyle y=mx+b$

$\displaystyle \begin{aligned} 1&=-2(-1)+b\\ \\ 1&=2+b\\ \\ b&=-1 \end{aligned}$

Therefore, the equation of the line has a slope ($m$) of $-2$ and a $y$-intercept ($b$) of $-1$.  The equation is $y=-2x-1$.

Example:  Write an equation of the line (in slope-intercept form) that is perpendicular to the line $y=\frac{1}{4}x-3$ and passes through the point $(2,4)$

Again, start with the slope-intercept form and substitute the values, except the value for the slope will be the negative reciprocal.  The negative reciprocal of $\frac{1}{4}$ is $-4$.  Therefore, the new equation has a slope of $-4$, through the point $(2,4)$.  Solve for $b$.

$y=mx+b$

$\displaystyle \begin{aligned} 4&=-4(2)+b\\ \\ 4&=-8+b\\ \\ b&=12 \end{aligned}$

Therefore, the equation of the line perpendicular to the given line has a slope of $-4$ and a $y$-intercept of $12$.  The equation is $y=-4x+12$.