A translation moves every point in a function a constant distance in a specified direction. In algebra, this essentially manifests as a vertical or horizontal shift of a function. A translation can be interpreted as shifting the origin of the coordinate system.

Vertical Translations

To translate a function vertically is to shift the function up or down. If a positive number is added, the function shifts up the $y$-axis by the amount added.  If a positive number is subtracted, the function shifts down the $y$-axis by the amount subtracted.  In general, a vertical translation is given by the equation:

$\displaystyle y = f(x) + b$

where $f(x)$ is some given function and $b$ is the constant that we are adding to cause a translation.

Let's use a basic quadratic function to explore vertical translations. The original function we will use is:

$\displaystyle y = x^2$. 

Translating the function up the $y$-axis by two produces the equation:

$\displaystyle y=x^2 + 2$

And translating the function down the $y$-axis by two produces the equation:

$y=x^2 - 2$.

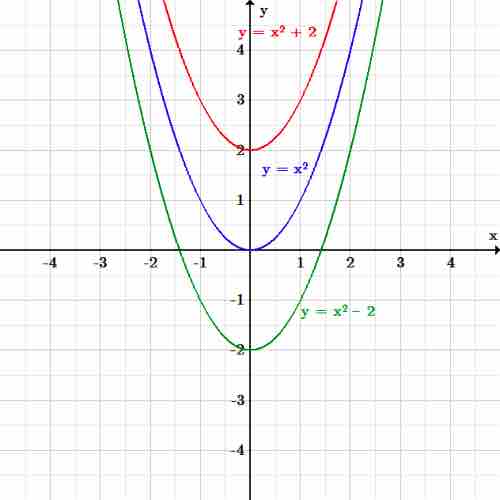
Vertical translations

The function $f(x)=x^2$ is translated both up and down by two.

Horizontal Translations 

To translate a function horizontally is the shift the function left or right. While vertical shifts are caused by adding or subtracting a value outside of the function parameters, horizontal shifts are caused by adding or subtracting a value inside the function parameters.  The general equation for a horizontal shift is given by:

$\displaystyle y = f(x-a)$

Where $f(x)$ would be the original function, and $a$ is the constant being added or subtracted to cause a horizontal shift.  When $a$ is positive, the function is shifted to the right.  When $a$ is negative, the function is shifted to the left.   

Let's use the same basic quadratic function to look at horizontal translations. Again, the original function is:

$\displaystyle y = x^2$.

Shifting the function to the left by two produces the equation:

$\displaystyle \begin{aligned} y &= f(x+2)\\ &= (x+2)^2 \end{aligned}$

Shifting the function to the right by two produces the equation:

$\displaystyle \begin{aligned} y &= f(x-2)\\ & = (x-2)^2 \end{aligned}$

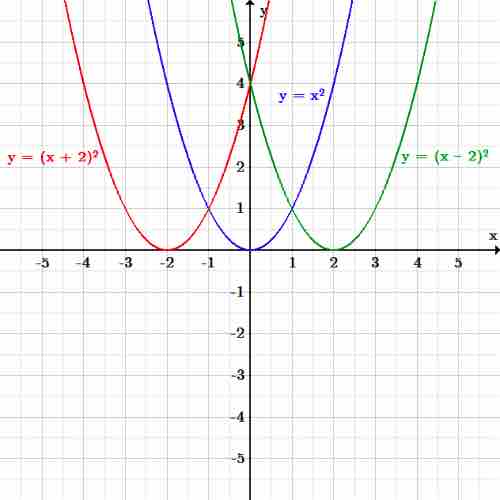
Horizontal translation

The function $f(x)=x^2$ is translated both left and right by two.