Reflections produce a mirror image of a function. The reflection of a function can be performed along the
Vertical Reflections
A vertical reflection is a reflection across the
In this general equation, all
The vertical reflection would then produce the equation:
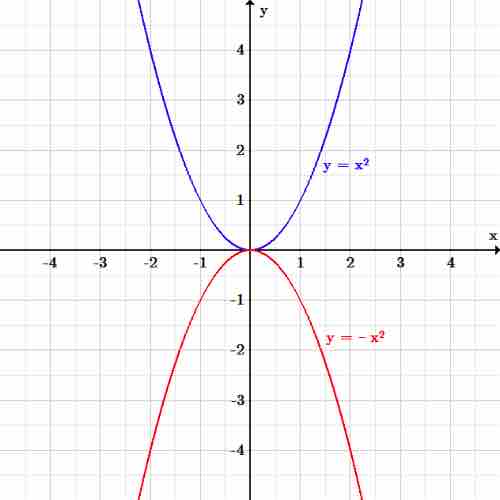
Vertical reflection
The function
Horizontal Reflections
A horizontal reflection is a reflection across the
In this general equation, all
Therefore the horizontal reflection produces the equation:
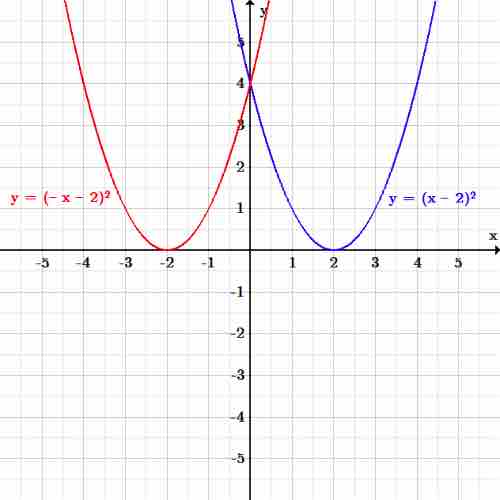
Horizontal reflection
The function
Reflections Across a Line
The third type of reflection is a reflection across a line. Let's look at the case involving the line
The reflected equation, as reflected across the line
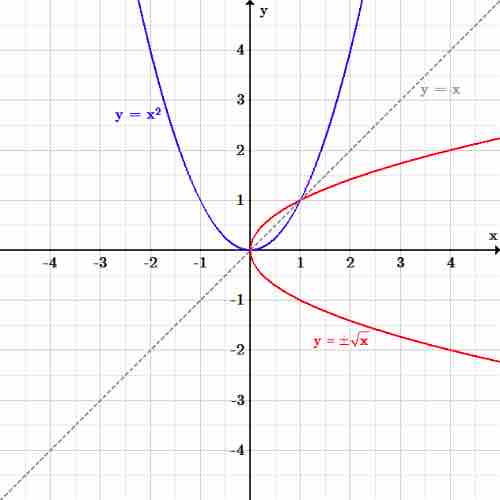
Reflection over $y=x$
The function