A transformation takes a basic function and changes it slightly with predetermined methods. This change will cause the graph of the function to move, shift, or stretch, depending on the type of transformation. The four main types of transformations are translations, reflections, rotations, and scaling.
Translations
A translation moves every point by a fixed distance in the same direction. The movement is caused by the addition or subtraction of a constant from a function. As an example, let
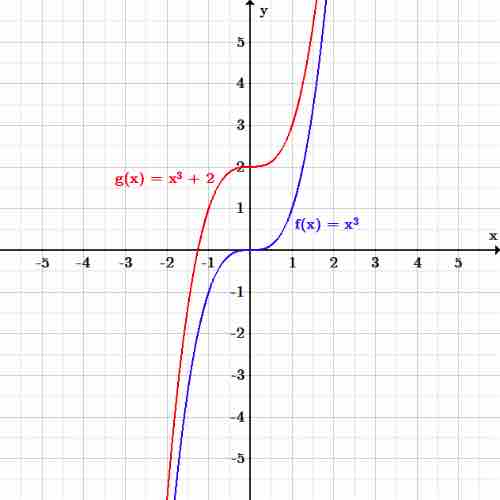
Graph of a function being translated
The function
Reflections
A reflection of a function causes the graph to appear as a mirror image of the original function. This can be achieved by switching the sign of the input going into the function. Let the function in question be
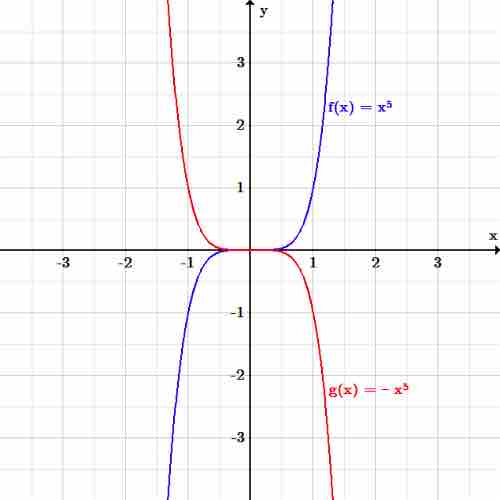
Graph of a function being reflected
The function
Rotations
A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotation. Although the concept is simple, it has the most advanced mathematical process of the transformations discussed. There are two formulas that are used:
Where
Scaling
Scaling is a transformation that changes the size and/or the shape of the graph of the function. Note that until now, none of the transformations we discussed could change the size and shape of a function - they only moved the graphical output from one set of points to another set of points. As an example, let
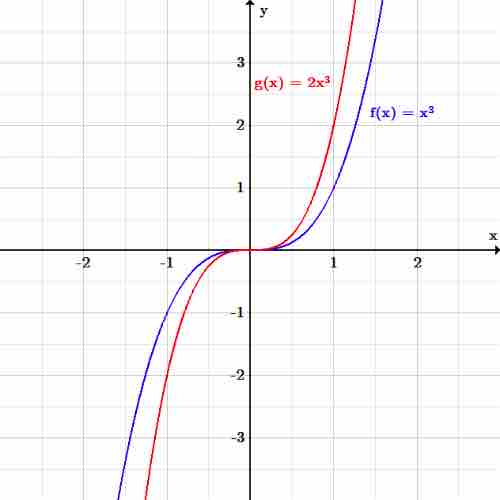
Graph of a function being scaled
The function