In mathematics, the vertical line test is a visual way to determine if a curve is a graph of a function, or not. Recall that a function can only have one output, $y$, for each unique input, $x$. If any $x$-value in a curve is associated with more than one $y$-value, then the curve does not represent a function. 

If a vertical line intersects a curve on an $xy$-plane more than once, then for one value of x the curve has more than one value of y, and the curve does not represent a function. If all vertical lines intersect a curve at most once then the curve represents a function.

Vertical Line Test

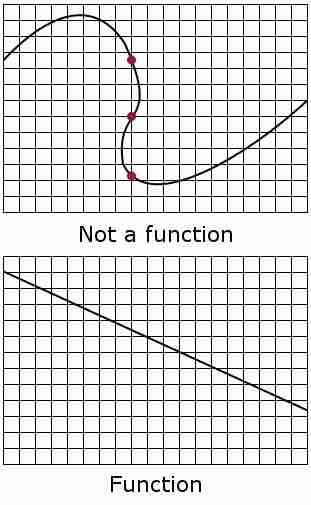
Note that in the top graph, a single vertical line drawn where the red dots are plotted would intersect the curve 3 times. Thus, it fails the vertical line test and does not represent a function. Any vertical line in the bottom graph passes through only once and hence passes the vertical line test, and thus represents a function.

To use the vertical line test, take a ruler or other straight edge and draw a line parallel to the $y$-axis for any chosen value of $x$. If the vertical line you drew intersects the graph more than once for any value of $x$ then the graph is not the graph of a function. If, alternatively, a vertical line intersects the graph no more than once, no matter where the vertical line is placed, then the graph is the graph of a function. For example, a curve which is any straight line other than a vertical line will be the graph of a function. 

Example

Refer to the three graphs below, $(a)$, $(b)$, and $(c)$. Apply the vertical line test to determine which graphs represent functions.

Applying the Vertical Line Test

Which graphs represent functions?

If any vertical line intersects a graph more than once, the relation represented by the graph is not a function. Notice that any vertical line would pass through only one point of the two graphs shown in graphs $(a)$ and $(b)$. From this we can conclude that these two graphs represent functions. The third graph, $(c)$, does not represent a function because, at most $x$-values, a vertical line would intersect the graph at more than one point. This is shown in the diagram below.

Not a Function

The vertical line test demonstrates that a circle is not a function.