What Is the Domain and Range of a Function?

The domain of a function is the set of input values, $x$, for which a function is defined. The domain is shown in the left oval in the picture below. The function provides an output value, $f(x)$, for each member of the domain.  The set of values the function outputs is termed the range of the function, and those values are shown in the right hand oval in the picture below.  A function is the relation that takes the inputs of the domain and output the values in the range. The rule for a function is that for each input there is exactly one output.  

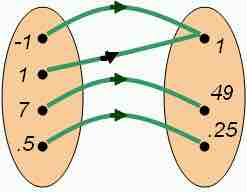
Mapping of a Function

The oval on the left is the domain of the function $f$, and the oval on the right is the range.  The green arrows show how each member of the domain is mapped to a particular value of the range.  

As you can see in the illustration, each value of the domain has a green arrow to exactly one value of the range.  Therefore this mapping is a function.  

We can also tell by the set of ordered pairs given in this mapping that it is a function because none of the $x$-values repeat: $(-1,1),(1,1),(7,49),(0.5,0.25)$; since each input maps to exactly one output.  (Note that although the output value of $1$ repeats, only the input values can not repeat)  

We can also tell this mapping, and set of ordered pairs is a function based on the graph of the ordered pairs because the points do not make a vertical line.  If an $x$value were to repeat there would be two points making a graph of a vertical line, which would not be a function.  Let's look at this mapping and list of ordered pairs graphed on a Cartesian Plane.

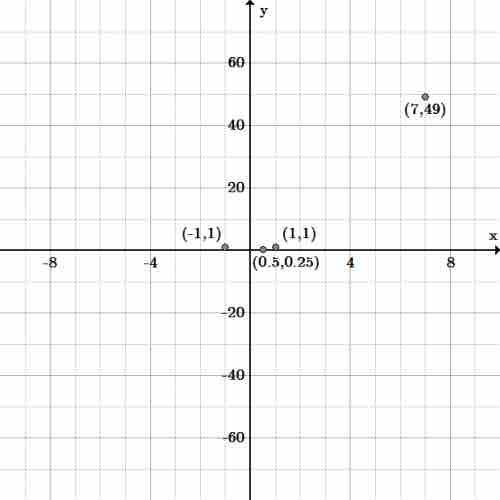
Ordered pairs

This mapping or set of ordered pairs is a function because the points do not make a vertical line.  This is called the vertical line test of a function.  It shows that for every input there is exactly one output value.

In addition, the domain of $f(x)=x^{2}$ is the set of all real numbers, $\mathbb{R}$ , as every real number you put into $f$ will give an output, namely $ x^2$.

It is important to note that not all functions have the set of real numbers as their domain. For instance, the function $f(x) = \frac{1}{x}$ is not defined for $x=0$, because you cannot divide a number by $0$. In this case, the domain of $f$ is the set of all real numbers except $0$. That is, $x\neq0$. So the domain of this function is $\mathbb{R}-\{0\}$ .

What about the function $f(x)=\sqrt{x}$ ? In this case, the square root of a negative number is not defined, and so the domain is the set of all real numbers where $x\geq0$ .

Finding the Domain and Range: Given a Function

In order to find the domain of a function, if it isn't stated to begin with, we need to look at the function definition to determine what values are not allowed. For instance, we know that you cannot take the square root of a negative number, and you cannot divide by $0$. With this knowledge in hand, let's find the domain of a function.

Example 1:  Find the domain of:

$\displaystyle f(x)=\frac{1}{\sqrt{x-1}-2}+x$  

First, we know we cannot divide by $0$, so any value of $x$ that causes a division by $0$ is not allowed in the domain. In this example, this occurs when:

$\displaystyle \sqrt{x-1}-2=0$ 

Solving for $x$, this happens when $x=5$, so we know that $x\neq5$ . 

We also know we can't take the square root of a negative number. This means that:

$\displaystyle x-1>0 $ 

After solving for $x$, we see that $x>1$. So this function's domain is the set of all real numbers such that $x>1$ and $x\neq5$. 

Therefore, to find what values are not in the domain, you must find the values where the function is not defined.