Definitions
At the most basic level, an exponential function is a function in which the variable appears in the exponent. The most basic exponential function is a function of the form
When
When
Graphing an Exponential Function
Example 1
Let us consider the function
As you connect the points, you will notice a smooth curve that crosses the
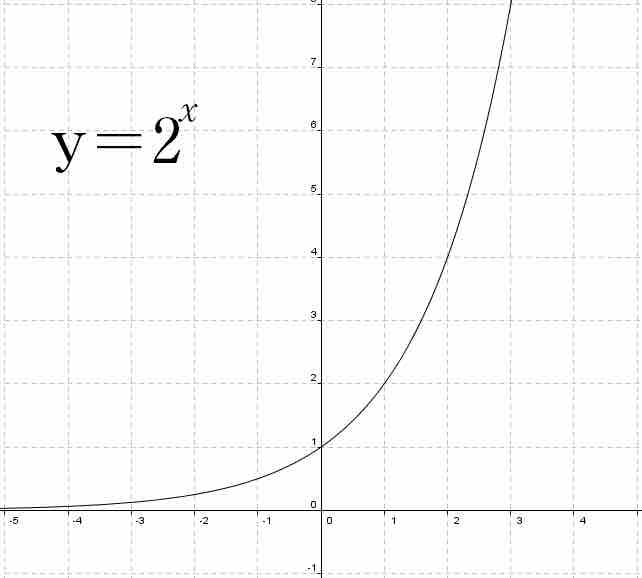
Graph of $y=2^x$
The graph of this function crosses the
Example 2
Let us consider the function
As you connect the points you will notice a smooth curve that crosses the y-axis at the point
As you can see in the graph below, the graph of
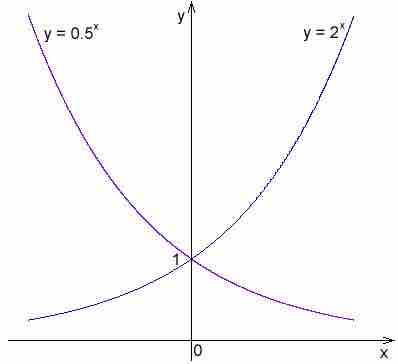
Graph of $y=2^x$ and $y=\frac{1}{2}^x$
The graphs of these functions are symmetric over the
Why Must $b$ Be a Positive Number?
If
If
Properties of Exponential Graphs
The point
The point
The function
The function