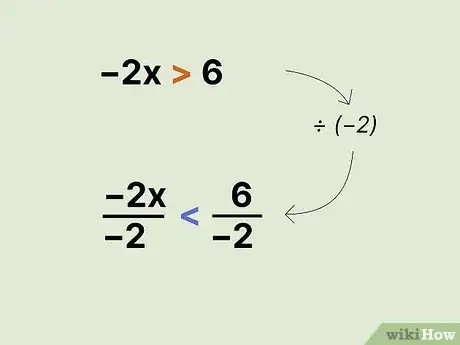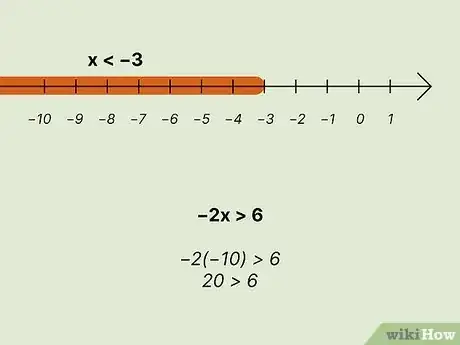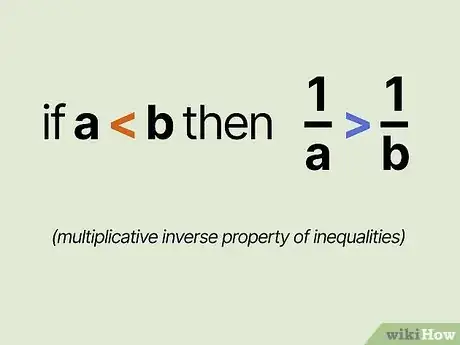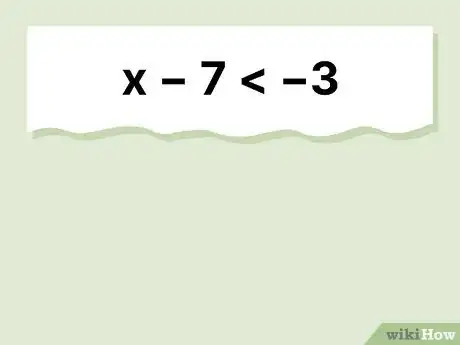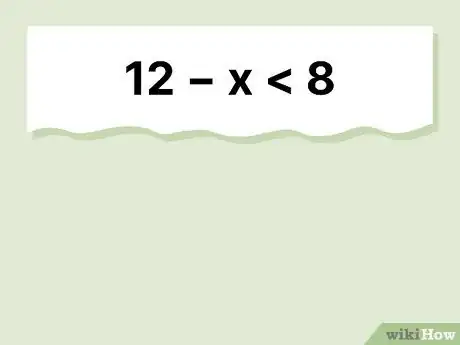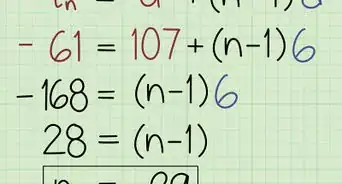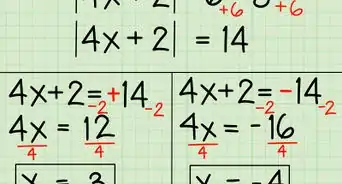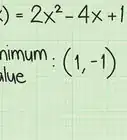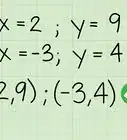Your Guide to Flipping the Inequality Sign (And Solving Inequalities)

Master inequalities with this super simple breakdown

Co-authored by Jennifer Mueller, JD

Last Updated: March 1, 2023 References

Solving Inequalities

|

Working with Reciprocals

|

Practice Problems

|

Solutions to Practice Problems

You're just getting the hang of solving basic equations, when all of a sudden that $=$ is a $>$ or a $<$ . Usually, you solve an inequality the same way you'd solve an equation, with one important difference—sometimes, you have to flip the inequality sign so it turns in the other direction. If you're not sure exactly when you need to do this, you're not alone! Read on to learn when you need to flip the inequality sign to solve an inequality correctly every time. You can even test your skills with some practice problems.

Things You Should Know

Solve inequalities using the same basic principles you use to solve equations.
Flip the inequality sign whenever you multiply or divide both sides by a negative number.
Flip the inequality sign if you take reciprocals on both sides of numbers that have the same sign (positive or negative).
Since the solution to an inequality represents a range of numbers, check several numbers in that range to make sure your solution is correct.

Section 1 of 4:

Solving Inequalities

1
Equations and inequalities follow the same basic principles. As a refresher, just like with standard equations, you'll want to isolate the variable on one side of the equation by dividing, multiplying, adding, and subtracting the same numbers from both sides of the equation.^{[1]
X
Research source}
- Unlike an equation, which leaves you with one final number as your answer, the solution to an inequality is a range of numbers. For example, if your solution is $x>4$ , that means any number greater than $4$ is a potential solution.
- When you check possible solutions to inequalities, you're trying to determine whether the statement made by the equality is true or untrue. If the statement is untrue, your solution is incorrect. For example, you might end up with $5<4$ . This is an untrue statement because 5 is not less than 4.
2
Reverse the inequality sign if you multiply or divide by a negative number on both sides. Addition and subtraction never change the direction of the inequality sign. Multiplication and division do change the direction of the inequality, but only if the number you're multiplying or dividing by is a negative number.^{[2]
X
Research source} See how this works with the inequality $-2x>6$ $-2x>6$ :
- To get the $x$ by itself, you have to divide by $-2$ . Since you're dividing by a negative number, you also have to flip the inequality sign: ${\frac {-2x}{-2}}<{\frac {6}{-2}}$ .
- Simplify on both sides of the inequality to get your solution: $x<-3$
Advertisement
3
Check more than one of the possible solutions. Unlike an equation, an inequality doesn't just have a single solution—it has many! Once you've solved an inequality, it's good practice to get in the habit of checking several of those possible solutions, just to make sure your answer is correct. If your solution is right, literally any number in the range should work—so pick numbers that are the easiest to quickly calculate in your head.^{[3]
X
Research source}
- To return to the previous example, the original inequality was $-2x>6$ and the solution was $x<-3$ .
- Start with $-3$ . Since the solution is less than $-3$ , you should get an equation here—and you do: $-2(-3)=6$ . So that checks out.
- Now try any number less than $-3$ , such as $-10$ : $-2(-10)>6$ simplifies to $20>6$ .
- In words, you would say "20 is greater than 6," and that's a true statement—so your solution checks out. Way to go!

Section 2 of 4:

Working with Reciprocals

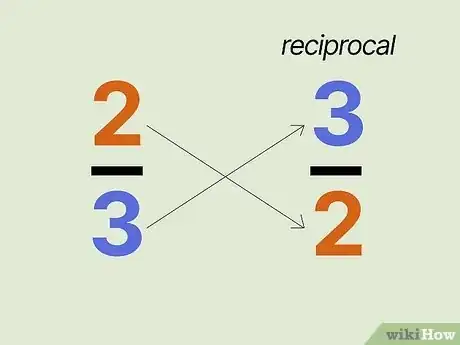
1
Flip a fraction upside-down to get its reciprocal. To take the reciprocal, you just reverse the position of the numerator and the denominator. So the reciprocal of the fraction ${\frac {2}{3}}$ ${\frac {2}{3}}$ would be ${\frac {3}{2}}$ ${\frac {3}{2}}$ . When you multiply a fraction by its reciprocal, you get $1$ $1$ .^{[4]
X
Research source} Watch how this happens:
- ${\frac {2}{3}}*{\frac {3}{2}}={\frac {6}{6}}=1$
- When you have a whole number, like $5$ , think of it as ${\frac {5}{1}}$ . That makes its reciprocal ${\frac {1}{5}}$ .
- Taking the reciprocal is also useful when you're solving for a variable in the denominator of a fraction. Taking the reciprocal on both sides allows you to get that variable by itself.
2
Reverse the inequality sign if you take the reciprocal of both sides. This is known as the multiplicative inverse property of inequalities. This property applies if both sides are positive or if both sides are negative. That's right, here you do it for positives as well—basically, any time the signs are the same on both sides.^{[5]
X
Research source} A simple example shows why this is true:
- Alex and Britt both run a 10k. Alex finishes first, running at 5 km/h, while Britt lopes along at a leisurely 2 km/h.
- Alex's speed is greater than Britt's speed: $5>2$ .
- To find out how long it took each of them to run the 10k, divide the distance by the speed: ${\frac {10}{5}}$ for Alex and ${\frac {10}{2}}$ .
- Simplify the fractions and you get $2$ and $5$ . Your inequality sign has reversed, because Alex finished the 10k in less time than Britt did.

Section 3 of 4:

Practice Problems

1
What is the solution to the inequality $-3x-42>3$ ?^{[6]
X
Research source}
2
Solve $x-7<-3$ for $x$ .^{[7]
X
Research source}
3
What is the solution to the inequality $12-x<8$ ?^{[8]
X
Research source}
4
Find the solution to the inequality $-3x<9$ .^{[9]
X
Research source}

Section 4 of 4:

Solutions to Practice Problems

1
The solution is $x<-15$ . Start by adding $42$ $42$ to each side of the equation, and you get $-3x>45$ $-3x>45$ . Now, you divide both sides by $-3$ $-3$ to isolate the variable. Since you're dividing by a negative number, you have to switch the signs: ${\frac {-3x}{-3}}<{\frac {45}{-3}}$ ${\frac {-3x}{-3}}<{\frac {45}{-3}}$ simplifies to $x<-15$ $x<-15$ . ^{[10]
X
Research source}
- Check your solution by using the end point of $-15$ : $-3(-15)=45$ . According to your solution, $x$ is less than $-15$ , so this shows your solution is correct.
2
The solution is $x<4$ . Start by adding $7$ $7$ to both sides to get the $x$ $x$ by itself: $x-7+7<-3+7$ $x-7+7<-3+7$ . Do the addition to get $x<4$ $x<4$ .^{[11]
X
Research source}
- Remember: no need to change the sign here because you never multiplied or divided by a negative number.
3
The solution is $x>4$ . Start by subtracting $12$ from each side to get $-x<-4$ . But since you need the value for $x$ , not $-x$ , multiply by $-1$ to find the positive value. Since you're multiplying by a negative number, though, you have to switch the sign, which gets you to $x>4$ .^{[12]
X
Research source}
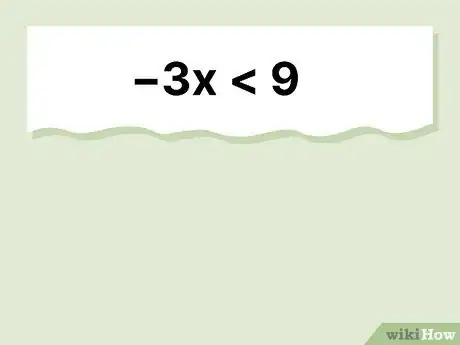
4
The solution is $x>-3$ . This problem is pretty simple—to get $x$ $x$ by itself, all you have to do is divide both sides by $-3$ $-3$ . But wait! Since you're dividing by a negative number, you also have to flip the sign.^{[13]
X
Research source}
- Plug in a value to test your solution: $-3(1)<9$ gives you $-3<9$ , which is a true statement!