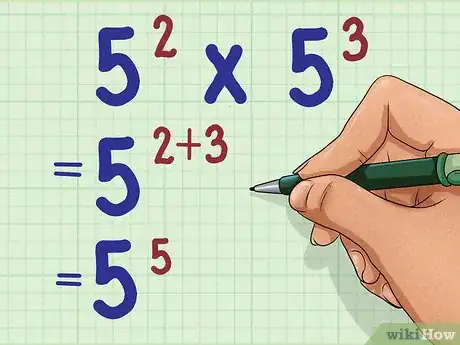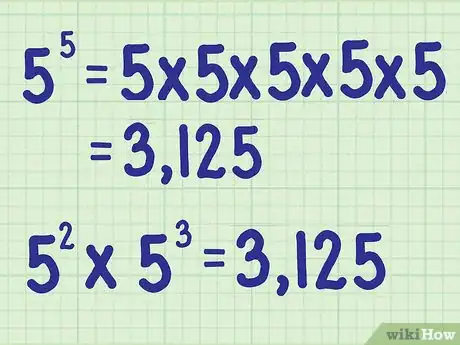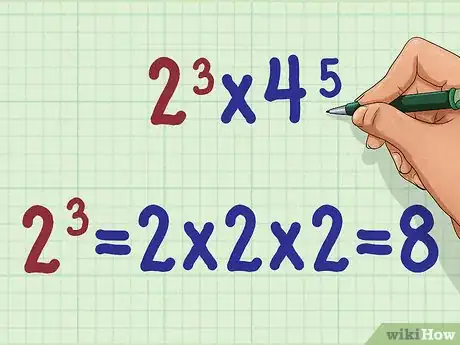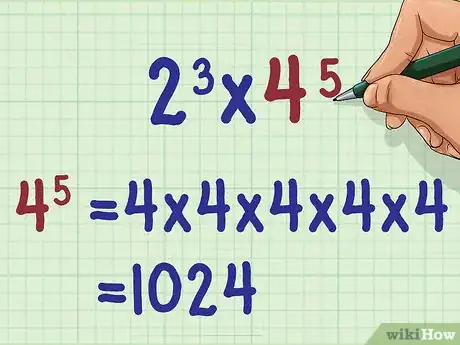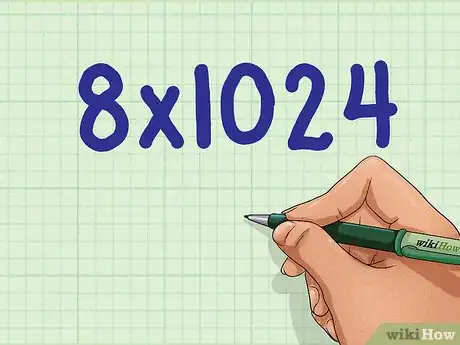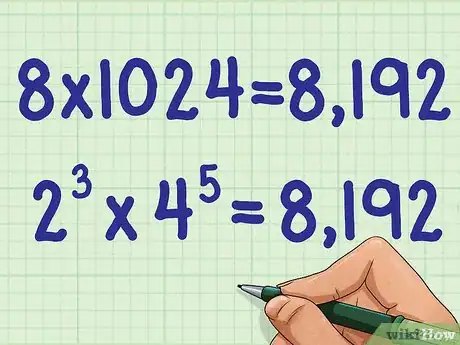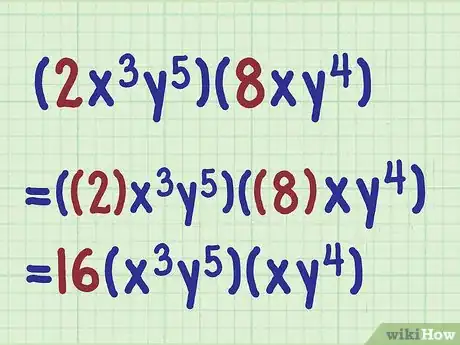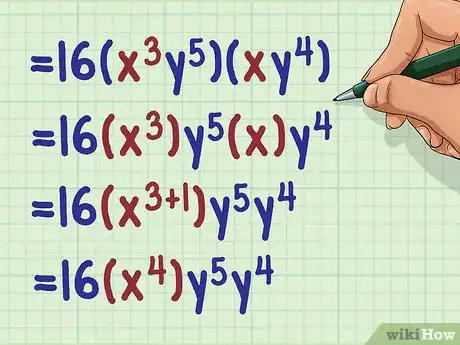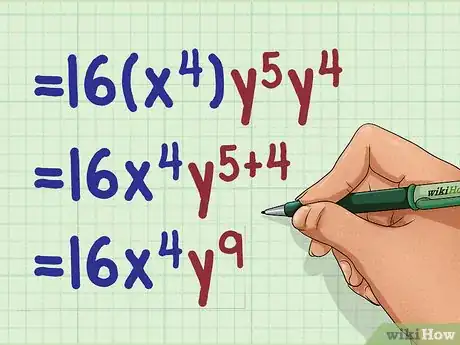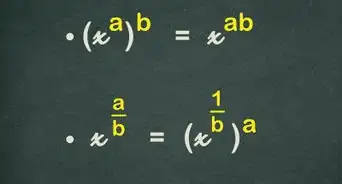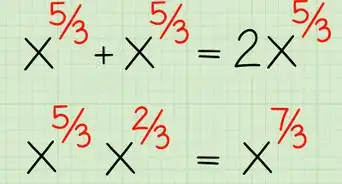This article was co-authored by David Jia. David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math.
This article has been viewed 81,591 times.
Exponents are a way to identify numbers that are being multiplied by themselves. They are often called powers. You will come across exponents frequently in algebra, so it is helpful to know how to work with these types of expressions. You can multiply exponential expressions just as you can multiply other numbers. If the exponents have the same base, you can use a shortcut to simplify and calculate; otherwise, multiplying exponential expressions is still a simple operation.
Steps
Multiplying Exponents with the Same Base
-
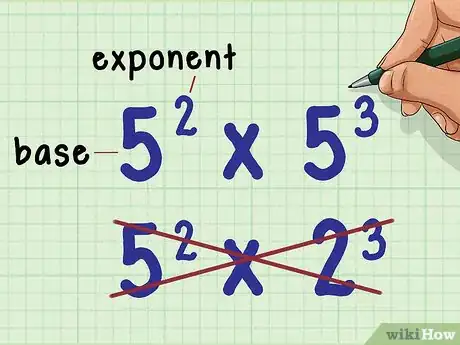
1Make sure the exponents have the same base. The base is the large number in the exponential expression. You can only use this method if the expressions you are multiplying have the same base.
- For example, you can use this method to multiply , because they both have the same base (5). On the other hand, you cannot use this method to multiply , because they have different bases (5 and 2).
-
2Add the exponents together. Rewrite the expression, keeping the same base but putting the sum of the original exponents as the new exponent.[1]
- For example, if you are multiplying , you would keep the base of 5, and add the exponents together:
Advertisement - For example, if you are multiplying , you would keep the base of 5, and add the exponents together:
-
3Calculate the expression. An exponent tells you how many times to multiply a number by itself.[2] You can use a calculator to easily calculate an exponential expression, but you can also calculate by hand.
- For example
So,
- For example
Multiplying Exponents with Different Bases
-
1Calculate the first exponential expression. Since the exponents have different bases, there is no shortcut for multiplying them. Calculate the exponent using a calculator or by hand. Remember, an exponent tells you how many times to multiply a number by itself.
- For example, if you are multiplying , you should note that they do not have the same base. So, you will first calculate .
-
2Calculate the second exponential expression. Do this by multiplying the base number by itself however many times the exponent says.
- For example,
-
3Rewrite the problem using the new calculations. Following the same example, your new problem becomes .
-
4Multiply the two numbers. This will give you the final answer to the problem.
- For example: So, .
Multiplying Mixed Variables with Exponents
-
1Multiply the coefficients. Multiply these as you would any whole numbers. Move the number to the outside of the parentheses.
- For example, if multiplying , you would first calculate .
-
2Add the exponents of the first variable. Make sure you are only adding the exponents of terms with the same base (variable). Don’t forget that if a variable shows no exponent, it is understood to have an exponent of 1.[3]
- For example:
- For example:
-
3Add the exponents of the remaining variables. Take care to add exponents with the same base, and don’t forget that variables with no exponents have an understood exponent of 1.
- For example:
- For example:
Community Q&A
-
QuestionWhat is the solution for 3.5 x 10 to the fourth power?
 Community Answer10^4 = 10 x 10 x 10 x 10 = 10,000, so you are really multiplying 3.5 x 10,000. The shortcut is that, when 10 is raised to a certain power, the exponent tells you how many zeros. 10^4 = 1 followed by 4 zeros = 10,000. Thus, you can just move the decimal point to the right 4 spaces: 3.5 x 10^4 = 35,000.
Community Answer10^4 = 10 x 10 x 10 x 10 = 10,000, so you are really multiplying 3.5 x 10,000. The shortcut is that, when 10 is raised to a certain power, the exponent tells you how many zeros. 10^4 = 1 followed by 4 zeros = 10,000. Thus, you can just move the decimal point to the right 4 spaces: 3.5 x 10^4 = 35,000. -
QuestionHow do I divide exponents that don't have the same base?
 Community AnswerTo learn how to divide exponents, you can read the following article: http://www.wikihow.com/Divide-Exponents
Community AnswerTo learn how to divide exponents, you can read the following article: http://www.wikihow.com/Divide-Exponents -
QuestionHow do I write 0.0321 in scientific notation?
 DonaganTop Answerer0.0321 = 3.21 x 10^(-2).
DonaganTop Answerer0.0321 = 3.21 x 10^(-2).
References
About This Article
If you want to multiply exponents with the same base, simply add the exponents together. For example 7 to the third power × 7 to the fifth power = 7 to the eighth power because 3 + 5 = 8. However, to solve exponents with different bases, you have to calculate the exponents and multiply them as regular numbers. For example, 2 squared = 4, and 3 squared = 9, so 2 squared times 3 squared = 36 because 4 × 9 = 36. To learn how to multiply exponents with mixed variables, read more!