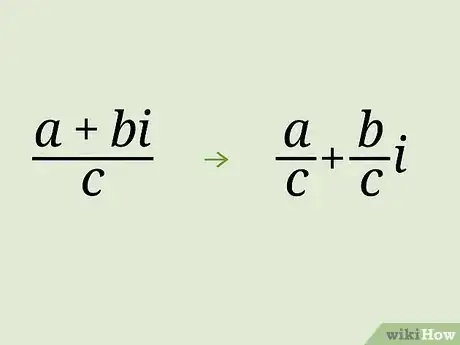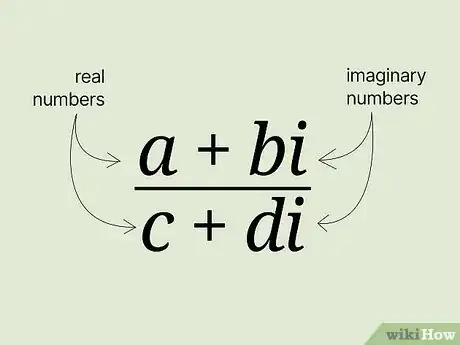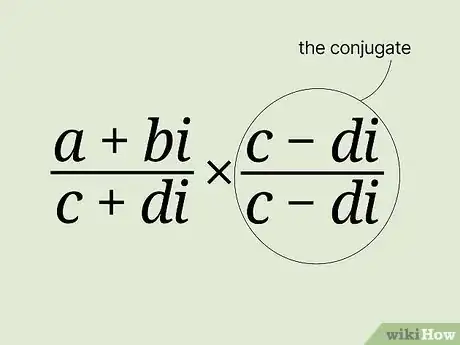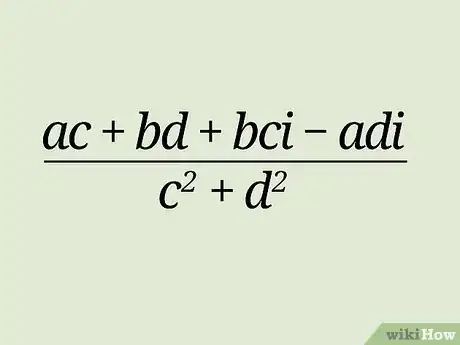Dividing Complex Numbers: A Quick Formula Guide

A handy guide to complex division for algebra

Written by Kyle Smith

Last Updated: March 20, 2023

Non-Complex Denominator

|

Complex Denominator

|

Tips

Dividing by a complex number doesn’t need to be complicated! You can easily simplify a complex fraction by multiplying by the complex conjugate of the denominator. This wikiHow shows you how to divide complex numbers.

Things You Should Know

Divide by a non-complex denominator by dividing each term in the numerator by the real number of the denominator.
Divide by a complex denominator by multiplying the numerator and denominator by the complex conjugate of the denominator.
This results in an expression with complex numbers only in the numerator.

Section 1 of 2:

Non-Complex Denominator

1
Examine the expression. If your numerator is a complex expression and your denominator is only a real number, you can expand the entire expression to simplify the fraction. It will take the following form:
- ${\frac {a+bi}{c}}$
- where $a$ and $c$ are real numbers and $bi$ is an imaginary number.
2
Expand and simplify the expression. This means dividing each term in the numerator by the denominator:
- ${\frac {a}{c}}+{\frac {b}{c}}i$
- Then, simplify the fractions to their decimal form.

Section 2 of 2:

Complex Denominator

1
Examine the expression. In this case, the numerator and denominator are complex. It will take the form:^{[1]
X
Research source}
- ${\frac {a+bi}{c+di}}$
- where $a$ and $c$ are real numbers, and $bi$ and $di$ are imaginary numbers.
2
Multiply by the complex conjugate. Since you can multiply any expression by 1 without changing it fundamentally, you can multiply the numerator and denominator by the conjugate of the denominator. This will simplify the entire expression so that only the numerator will have complex numbers.
- The conjugate has the form:
  - ${c-di}$
- Multiply by the conjugate:
  - ${\frac {a+bi}{c+di}}*{\frac {c-di}{c-di}}$
3
Simplify the expression. Multiplying the numerator and denominator by the complex conjugate will result in:
- ${\frac {ac+bd+bci-adi}{c^{2}+d^{2}}}$
- Note that during the simplification process, multiplying two complex numbers means squaring $i$ , resulting in $-1$ .
- Further simplify the complex numbers by adding the real and complex numbers and dividing each numerator term by the denominator.