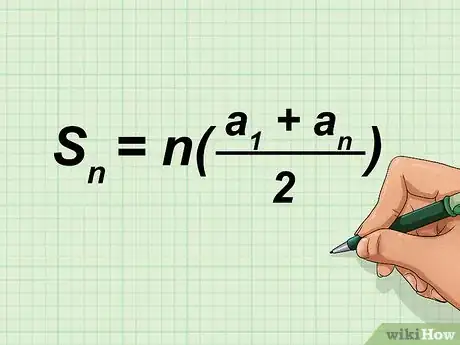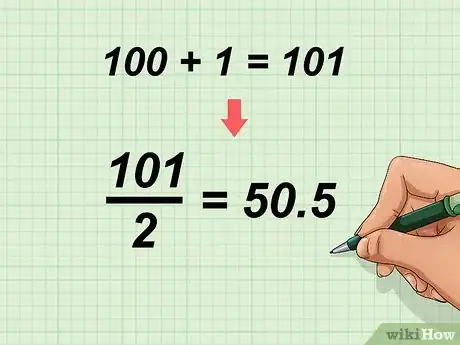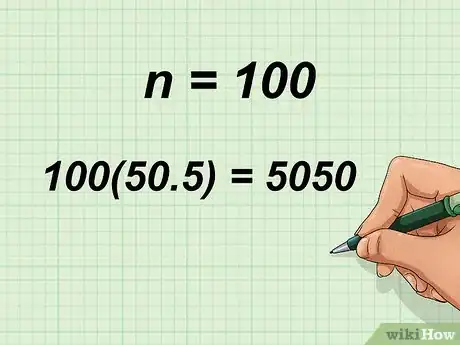This article was co-authored by wikiHow Staff. Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards.
This article has been viewed 84,214 times.
Learn more...
According to math legend, the mathematician Carl Friedrich Gauss, at the age of 8, came up with a method for quickly adding the consecutive numbers between 1 and 100.[1] The basic method is pairing numbers in the group, then multiplying the sum of each pair by the number of pairs. From this method we can derive a formula for adding consecutive numbers through : . These methods can be applied to any series of consecutive numbers, not just 1 through 100.
Steps
Using the Formula for the Sum of a Series
-
1Write the formula for finding the sum of an arithmetic series. The formula is , where equals the number of terms in the series, is the first number in the series, is the last number in the series, and equals the sum of numbers.[2]
-
2Plug the values into the formula. This means substituting the first term in the series for , and the last term in the series for . When adding consecutive numbers 1 through 100, and .
- Thus, your formula will look like this: .
Advertisement -
3Add the values in the numerator of the fraction, then divide by 2. Since , you will divide 101 by 2: .
-
4Multiply by . This will give you the sum the consecutive number in the series. In this instance, since you are adding consecutive numbers to 100, . So, you would calculate . Thus, the sum of the consecutive numbers between 1 and 100 is 5,050.[3]
- To quickly multiply a number by 100, move the decimal point two places to the right.[4]
Using Gauss’s Technique
-
1Divide the series into two equal groups. To find out how many numbers are in each group, divide the number of numbers by 2. In this instance, since the series is 1 to 100, you would calculate .[5]
- So, the first group will have 50 numbers (1-50).
- The second group will also have 50 numbers (51-100).
-
2Write the first group, 1-50, in ascending order. Write the numbers in a row, beginning with 1 and ending with 50.[6]
-
3Write the second group, 100-51, in descending order. Write these numbers in a row under the first group. Begin so that 100 lines up under 1, 99 lines up under 2, etc.[7]
-
4Add each vertical set of numbers. This means you will calculate , . etc. You don’t actually have to add up all the sets of numbers, because you should see that each set adds up to 101.[8]
-
5Multiply 101 times 50. To find the sum of consecutive numbers 1 to 100, you multiply the number of sets (50) by the sum of each set (101): So, the sum of consecutive number 1 through 100 is 5,050.[9]
Community Q&A
-
QuestionWhat is the total if I add up all numbers from 1 to 300?
 DonaganTop Answerer
DonaganTop Answerer -
QuestionWhat are the consecutive numbers that add up to 100?
 Community AnswerYou need to know how many consecutive numbers you are looking for and then use algebra to solve. For example, if you know you are looking for 5 numbers, you would set up the equation x + (x + 1) + (x + 2) + (x + 3) + (x + 4) = 100. Then, simplify: 5x + 10 = 100; 5x = 90; x = 18. So, the five consecutive numbers are 18, 19, 20, 21, and 22.
Community AnswerYou need to know how many consecutive numbers you are looking for and then use algebra to solve. For example, if you know you are looking for 5 numbers, you would set up the equation x + (x + 1) + (x + 2) + (x + 3) + (x + 4) = 100. Then, simplify: 5x + 10 = 100; 5x = 90; x = 18. So, the five consecutive numbers are 18, 19, 20, 21, and 22.
References
- ↑ https://nzmaths.co.nz/gauss-trick-staff-seminar
- ↑ https://www.cuemath.com/sum-of-arithmetic-sequence-formula/
- ↑ https://mathworld.wolfram.com/ArithmeticSeries.html
- ↑ https://www.khanacademy.org/math/5th-engage-ny/engage-5th-module-1/5th-module-1-topic-a/v/multiplying-a-decimal-by-a-power-of-10
- ↑ https://letstalkscience.ca/educational-resources/backgrounders/gauss-summation
- ↑ https://nzmaths.co.nz/gauss-trick-staff-seminar
- ↑ https://nzmaths.co.nz/gauss-trick-staff-seminar
- ↑ https://letstalkscience.ca/educational-resources/backgrounders/gauss-summation
- ↑ https://nrich.maths.org/2478