Won't all hashes collide after enough iterations with a static salt?

Question

We all know that we're supposed to take a fairly slow hashing algorithm, salt the password, and run the hash for many iterations. Let's say that I'm following almost everything except for one rule, and I have a static salt. Something like this:

password = 'yaypuppies' + some_static_salt

1000.times do
    password = amazing_hash(password)
end

And now password is a great hashed and salted thing. All is well with the world.

But what if we ran it a whole lot more iterations?

3000000000000000000.times do # 3 quintillion
    password = amazing_hash(password)
end

Would, in theory, many passwords collide? I.e. would this happen?

pass1 -> lkajsdlkajslkjda > 23oiuolekeq > n,mznxc,mnzxc > common_thing > 987123oijd > liasjdlkajsd > 09893oiehd > 09uasodij
pass2 -> loiuoklncas > 9830984cjlas > ioasjdknckauyieuh > common_thing > 987123oijd > liasjdlkajsd > 09893oiehd > 09uasodij

And both passwords end up hashed to 09uasodij?

With a non-randomized-per-password salt, does the chance of a collision go up with every iteration added?

Answer 1

When iterating a hash function, space reduction occurs, but not down to a single point. For a randomly chosen function (that your "amazing_hash" is supposed to approach), with a n-bit output, you may expect to ultimately reach a cycle of size 2^n/2 or so, i.e. still big enough if you use a decent output size (say, n = 256).

See this answer for more detailed explanations. I reproduce here the scheme from that answer, because it is a good eye-catcher:

Of course, a "static salt" is not a salt; it just means that you are using a custom hash function. The salt is meant to deter parallel attacks: when the attacker tries to crack 10 passwords, it costs him 10 times the cost of cracking one. With a "static salt", cracking 10 passwords costs no more than cracking 1, i.e. a total failure of the salting.

Salts are not about avoiding collisions, notably because collisions are not a problem for password hashing. It is preimage resistance that you should worry about.

Answer 2

I don't think so, just because the hash would almost certainly reach "common_thing" at different points. One password might has to "common_thing" at step 10,000, and another at step 100,000. The chains will track each other in parallel, but they won't necessarily be at the same point when the algorithm ends.

Whether the cycles are large or small, the probability is still low. If there are many small cycles, a value is less likely to end up in any particular one of them; if there are a few large cycles, the value is less likely to end the chain at the same point.

As other people have said, the reason you don't use a static salt is to keep attackers from creating rainbow tables. I'm not sure that the static salt has any effect on the number of collisions over time, other than that of course identical values will hash to the same value.

Take all this with a grain of salt, though; I'm a crypto enthusiast, but not an expert. I'd love to hear more about cycles in hash algorithms if other people are more informed in this area.

Answer 3

The issue related to the static salt, is not that there are increased chances of collision (there is not). Running the same algorithm repeatedly will not lead to an increase in collisions (with a good hashing function) just so long as all passwords have the same number of iterations.

The real issue is a game of odds.

If an attacker knows the code used to generate the hashed password (the mechanism used to inject the salt, and the number of iterations through the hash loop), then the attacker can reproduce your algorithm. Assume that the attacker also knows your actual hashed result. Can they work out your actual password?

With the algorithm, the attacker can then feed a dictionary of common passwords in to the algorithm, and look for matches to your hashed result. Admittedly, it may take a long time, but, eventually the attacker could guess your password.

The thing is, that you may have a 'hard to guess' password.... but, what about everyone else in the system. Your hashed password is just one of many. If the site is 'stack exchange', then there are thousands of users. If they all use the same salt, then, a dictionary attack like this can check for the match against all the users' hashed passwords. If they get a match, then they have also guessed that user's password. It's a numbers game. If there are 10,000 users in a system, then the odds of finding an easy password are improved by 10,000, likely much more than that.

Now, if you use a unique salt for each user, getting a matching hash for a user is useless unless that user also has the same salt you have in your algorithm.

In other words, with a unique salt, you can only attack one user account at a time. With a static salt, you can attack them all at once.... and the chances of a hit are much greater.

Answer 4

In theory, yes, that will definitely happen, for sufficient definitions of "a whole lot" and "many". In practice, no, that will never happen. The point of a secure cryptographic hash function is that "a whole lot" and "many" are ridiculously large numbers that cannot be reached. If you can reach them, either there's a severe attack against the algorithm, and you shouldn't use it, or it's not big enough, and you shouldn't use it.

For example, take MD5. A hash is 128 bits long. Ideally, on average you should find one collision with 2⁶⁴ tries, or about 18 quintillion. This would be very expensive, but possible to do with enough hardware. However, MD5 has suffered catastrophically from cryptanalysis, and there are attacks that can find collisions in moments.

On the other hand, there's SHA-256. It's 256 bits -- it's not possible to calculate 2¹²⁸ hashes, and there aren't significant attacks against it.

So this is not a concern if you're using a decent hash like SHA-256 or SHA-512. It also shouldn't be a concern even if you're not. I can't think of why a user would try to create a password that intentionally causes a collision, and it's not practical to use a significant number of iterations, unless you want it to take decades of calculation for your users to log in. (This is aside from the considerations mentioned in the other answers.)

Essentially, my question is: With a non-randomized-per-password salt, does the chance of a collision go up with every iteration added?

Yes, it does, from "so close to zero it will never happen" to "still so close to zero it will never happen".

Answer 5

As far as the theory goes, each output of the function amazing_hash has a fixed size, and is mapped to another output of the hash function, and another, and so on.

So, leaving aside the very first input, you have a function from a finite set to itself. The function may or may not be bijective, but it's not a required property of a hash function that it is. The domain of the function necessarily is divided up into:

• one or more cycles, plus
• zero or more "tails", that is to say sequences that lead into one of the cycles or into another tail. When two tails join consider it arbitrary which one is leading into the other one, but I'm going to use the number of tails later, so it has to be defined that way :-) Define also the "end" of a tail to be the point where it joins another tail or a cycle.

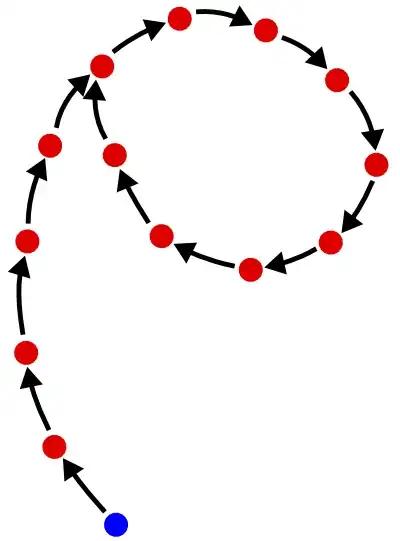
Every point, when iterated, is either part of a cycle to begin with or else it follows a tail, and the tails that tail joins, until it joins a cycle. That's a necessary property of a function from a finite set to itself. A path cannot run forever without entering a cycle, because there are only finitely many values and so eventually it must repeat one. You can therefore imagine the function visually as a lot of circles, with branches sticking out of the sides of them. The branches all lead into the circles.

With one iteration (that is, one further hash after the initial hash), how many collisions are there? Well, it's related to the number of tails, since the end of a tail is a place where two non-equal values have the same hash. Each join point implies there is a number of colliding values equal to the number of structures joining at that point. Every tail ends in a join, so if we define "tails" and "collisions" carefully then the number of collisions is just the number of tails.

After two iterations, how many collisions are there? It's the number of tails (since once two values are collided they stay collided), plus the number of new collisions caused by the extra iteration. The extra iteration causes a collision if "both sides" of a join point are at least 2 nodes long. So where two tails join they must both be at least 2 nodes long, and where a tail joins a cycle it must be at least a 2-cycle.

After n iterations, further collisions are generated by tails at least n nodes long, and n-cycles.

In the extreme case, a hash function that is bijective has no tails. This is theorem one of finite functions: every permutation partitions its domain into cycles. Then it should be easy to see that no matter how many iterations you do, there are no collisions (other than those caused by the initial hash, of course). Each point just moves around its cycle. By moving every point an equal number of steps around a cycle, they're still all in different positions.

Otherwise, to begin with the more iterations you do, the more collisions get generated as the tails merge into the cycles. However, there is an upper limit to this process, because every tail and every cycle has a finite length. Eventually you will cause no more collisions when you do more iterations. That won't happen until you've reached the length of the longest tail in your function.

This is all in theory: in practice the longest tail might still be rather larger than you have time to iterate. If so you would keep increasing the number of collisions for as long as you can practically run.

However, the number of collisions that each iteration introduces is still very small compared to the hash space, so small that it's incredibly unlikely you'll encounter a collision this way. How do we know this? Because if it wasn't, then Floyd's cycle-finding algorithm would be an effective means to find collisions in the hash function. The hash function would not be "amazing" per the assumptions of the question, it would be known to be broken :-)

Answer 6

Would, in theory, many passwords collide?

In your example, what you are looking at is how easy is it for two inputs to get the same output, known as collisions. This is an important area in cryptography, is used to evaluate the strength of the algorithms, and varies for every algorithm.

The number of iterations does not matter, even in your example, because all that is interesting is the following:

hash(n,mznxc,mnzxc)     > common_thing 
hash(ioasjdknckauyieuh) > common_thing 

Since you are taking the output of a hash and then pushing it back as the input, the input and output are the same size (except for the very first input).

Algorithms, such as MD5, are known to have been shown some collision vulnerabilities. MD5 collisions are also known to have been exploited in the Flame virus, even though when MD5 was invented as a secure replacement of MD4. And thus, cryptography relies on review and research of a large number of cryptographers to figure out which algorithms have not yet shown any weaknesses.

Thus, at any point in time, you have to look at which hash functions do not have any known vulnerabilities, and design your system such that in the future, you can rollover the hash function (i.e. be crypto-agile).

With a non-randomized-per-password salt, does the chance of a collision go up with every iteration added?

Non-randomized salts do not solve this problem. They solve the issue of rainbow tables and password collisions (i.e. if two users have the same salt, same password and same number of iterations, you get the same hash.) From a design perspective, you must assume that the salt and number of iterations are publicly known (even if you manage to hide them).

Given that many users share the same passwords ("123456", "password", "abcdefgh", etc.), with non-randomized salts and iterations, predicting passwords becomes much easier using frequency analysis due to same hashes resulting from same passwords.

Answer 7

So, put simply: what are the odds of input A and input B hashing to the same thing after N iterations? (The salt doesn’t change anything about this.) Because H(A) and H(B) should be uniformly randomly distributed for a good hash function, this is about the same as the odds of H(A) and H(B) not colliding times the odds of H(A) and H(B) not colliding after N − 1 more rounds. For SHA-256 with 2²⁵⁶ possible outputs (ideally), that’s 1 − ((2²⁵⁶ − 1)/2²⁵⁶)^N ≈ 2.59 × 10⁻⁵⁹ for 3 quintillion iterations.

That’s not very likely.

You can also estimate the probability of going into the loop that other answers have mentioned with the birthday problem approximation, though, as other answers have also mentioned, that won’t cause a collision unless the two inputs are synchronized in this loop.

For SHA-256 and 3 × 10¹⁸ iterations again, that’s 1 − e^{−(3 × 1018)2/(2 × 2256)} ≈ 3.89 × 10⁻⁴¹.

Also not very likely.

Answer 8

No.

It's all about entropy.

Given a "non-broken" cryptographic hash function, it produces N bits of pseudorandom output for any input of length M, which is nothing but extracting N bits of entropy out of those M bits.¹
Of course this only works in a reasonable way if M >= N, since you can hardly extract N bits of entropy if the input doesn't contain that much at all.

The likelihood of collisions is described by the well-known birthday paradoxon (which ironically does not at all work with actual birthdays, since these are very unevenly distributed!).
The likelihood for users choosing identical passwords is much, much higher than that. Or put differently, the entropy contained in a user password (even a relatively good one) is abysmal.

Salt adds entropy to the input. Which means that the first iteration with a static (I assume that "static" still means "per user"!) actually reduces the likelihood of a collision as compared to the plain password.

Now what happens on the second, third, and ith iteration? The hash function takes as input the output of the previous round, which contains N bits of entropy (which already includes the entropy in the static salt, so appending the salt again still leaves it at N), and it outputs N bits of entropy.
The CPU spins, bits flip around, the numbers look different, but nothing changes as far as entropy or collision likelihood is concerned. N bits in, N bits out.

So no, it does not get worse (but also, it doesn't get better).

---

¹ This is, for example, the reasoning behind DJB telling you to hash the key that you get from your curve25519 function a few times (in addition to making an attack on the EC much harder). The curve has a strength of ca. 128 bits, and the function outputs a string of 32 bytes. Which means you have a blob of 256 "random looking" bits with only 128 bits of actual entropy inside, but you have no clue where it is. Which bits do you use? Hashing the 256 bits into 128 bits solves the problem elegantly without risking to throw away useful bits.