Why removing just one letter form passwords makes it 20x easier to break according to zxcvbn test

Question

Since I am a decent fan of the XKCD no 936 (or actually conclusions and implications it brings), I wanted to test (using try zxcvbn) the complexity and the possiblity of breaking a password like the following one:

My password for Facebook

Written in my own native language (Polish), that is:

Moje hasło do Facebooka

The original password is marked by zxcvbn as... well not so easy to break:

But what actually surprised me the most was finding out that removing just a single letter from the middle of this password:

Moje hasło do Facebooka → Moje asło do Facebooka

causes this password to be approx. 20 times easier to break (again, according to zxcvbn):

Assuming that "centuries" means "at least 2 centuries", so at least 300 years, then by getting down to 15 years (on the list item: 10B guesses / second; offline attack, fast hash, many cores) gives us 20 times degrade on power strength, if I am not mistaken.

Why is that? Why removing just one letter (in this scenario or in general) makes password so easier to break?

Answer 1

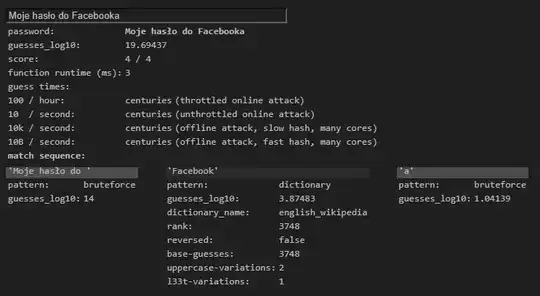
The password entropy calculation from this tool is not very accurate and is generating values I consider to be too high. That said, removing a character from a passcode will reduce its complexity by the number of iterations that character represents. Assuming the Polish alphabet's 32 letters (or 35 if including q, v, and x), your shorter password would make the password 32x (or 35x) easier to break, at least when missing the fact that this is a passphrase composed of words.

Password complexity detection tools are all wrong.

Password complexity cannot be calculated without knowing the formula used to create the password. Guessing that formula can be disastrous, as you have experienced with this tool.

Your Moje hasło do Facebooka password appears to use a formula of "four Polish words". This is not a good formula. When composing a passphrase, you must ensure that the words are randomly generated and not related to each other. "My password for Facebook" is a sensible sentence, so it is not a good password. (See also the infosec.SE analysis xkcd 936 for correct horse battery staple.)

If your password, quoted, might have hits in a Google search, it is not secure.
(This is an intellectual exercise; don't share potential passwords with a search engine.)

Let's instead assume your password was Poprawny koń zszywka bateria. The first thing you'll notice is that I translated each word separately rather than properly conjugating it as "Prawidłowa bateria zszywek dla koni". This is because the words must not be related to each other. In languages with grammatical gender, this might be a little confusing, but it's important because otherwise you're losing entropy. This is also why the English passphrase isn't "Correct horses staple batteries" or something else that's more of a sentence (the plural "horses" implies a plural for "batteries").

The complexity of this comes from the size of the dictionary. If you're using a standard English spelling dictionary, that's 100k. The Polish dictionary I just downloaded has 4000k, though that might be implausible; I just auto-generated a passphrase of ontologi trzebieszowskie niefortecznej nielitogeniczną, which seems like quite a mouthful.

There's a password-generation system called diceware, which has its own Polish diceware word list you could use. Example passphrase: plewka szpieg raban pruski ibi.

Diceware has a 7776-word dictionary, so a four-word diceware passphrase has an entropy of log₂(7776⁴) = 51.

This tool seems to ignore standard entropy measurement in bits truncated to an integer and instead measures in base 10, so log₁₀(7776⁴) = 15.56303.

Reducing a passphrase like plewka szpieg raban pruski ibi down to plewka zpieg raban pruski ibi actually increases its complexity since zpieg is not a word. In my own entropy calculations, I multiply words by six for typos/misspellings or iterations like l33t speak, so the entropy goes up by a little, from log₂(7776⁵) = 64 to log₂(7776⁵×6×5) = 69 assuming the attacker knows you've varied one word but not which one.

(Always assume attackers know your formula. Hopefully, they don't and will therefore take far longer to break your password, but calculating complexity needs to assume the worst-case scenario or else you're just hiding in presumed obscurity.)

Answer 2

Your first password Moje hasło do Facebooka is 24 characters in length. Your second password Moje asło do Facebooka is 23 characters in length.

Assume that both passwords were constructed by randomly selecting characters from a set of 20 symbols. In the first case, this was repeated 24 times, to create a random password of 24 characters in length. In the second case, this was repeated 23 times, to create a random password 23 characters in length.

We use the term 'password space' to denote the number of possible passwords that can be created using this random process.

In the first case, the password space is 20^24 (24 characters, where each character can be one of 20 possible symbols), whereas in the second case, the password space is 20^23. Therefore, the password space in the first case is 20 times greater than the password space in the second case, because 20^24 / 20^23 = 20. So, the 24 character password is 20 times harder to crack than the 23 character password, because it is in a space that is 20 times larger.

Answer 3

There are 35 letters in the Polish alphabet. If your password consists of a single lower case Polish letter, there are 35 possible passwords. If the password consists of 2 Polish letters and if these letters are chosen randomly, independent on each other, there are 35 possible letters on the 1st place and for each of them there are 35 possible letters on the 2nd place. Thus there are 35 x 35 possible passwords. To check all of them, you need 35 times more time than to check a password that consists of a single letter. Thus, adding a letter to password increases the number of possible passwords in 35 times. Means, an attacker will need 35 times more time to check all possible passwords.

This works also vice versa. If you have some password and make it shorter by one letter, the attacker will need 35 times less time to check all of them.

If you use lower and upper case, there are actually 35 x 2 = 70 possible letters on each position. If you use space character, there are 71 possible letters on each position. Adding or removing a single character in such case increases or reduces the brute-forcing time in 71 times.