Review of Domain, Range, and Functions

As stated in a previous section, the domain of a function is the set of 'input' values $(x)$ for which the function is defined.  The domain is part of the definition of a function.  For example, the domain of the function $f(x) = \sqrt{x} $ is $x\geq0$.

The range of a function is the set of results, solutions, or 'output' values $(y)$ to the equation for a given input.  By definition, a function only has one result for each domain.  For instance, the function $f(x)=x^{2}$ has a range of $f(x)\geq0$, because the square of a number always yields a positive result.

In taking both domain and range into account, a function is any mathematical formula that produces one and only one result for each input. Hence, every given domain value has one and only one range value as a result, but not necessarily vice versa. In other words, two different values of $x$ can have the same $y$-value, but each $y$-value must be joined with a distinct $x$-value.  This makes sense since results can repeat (the $y$-values), but inputs cannot (the $x$-values).

Determining Domain and Range 

The domain and range can be visualized using a graph, such as the graph for $f(x)=x^{2}$, shown below as a red U-shaped curve.  The blue N-shaped (inverted) curve is the graph of $f(x)=-\frac{1}{12}x^3$.  

Example 1:  Determine the domain and range of each graph pictured below:

Both graphs include all real numbers $x$ as input values, since both graphs continue to the left (negative values) and to the right (positive values) for $x$ (inputs).  The curves continue to infinity in both directions; therefore, we say the domain for  both graphs is the set of all real numbers, notated as: $\mathbb{R}$. 

If we now look at the possible outputs or $y$-values, $f(x)$, (looking up and down the $y$-axis, notice that the red graph does NOT include $y$-values that are negative, whereas the blue graph does include both positive and negative values.  Therefore, the range for the graph $f(x)=x^{2}$, is $\mathbb{R}$ except $y< 0$, or simply stated: $y \geq 0$.  The range for the graph $f(x)=-\frac{1}{12}x^3$, is $\mathbb{R}$.

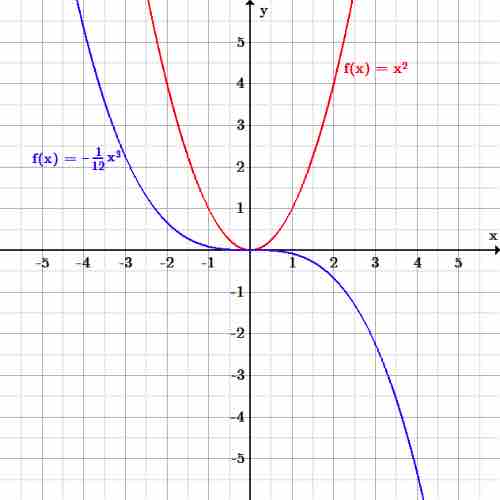
Domain and range graph

The graph of $f(x)=x^2$ (red) has the same domain (input values) as the graph of $f(x)=-\frac{1}{12}x^3$ (blue) since all real numbers can be input values.  However, the range of the red graph is restricted to only $f(x)\geq0$, or $y$-values above or equal to $0$.  The range of the blue graph is all real numbers, $\mathbb{R}$.

Example 2: Determine the domain and range of each graph pictured below:

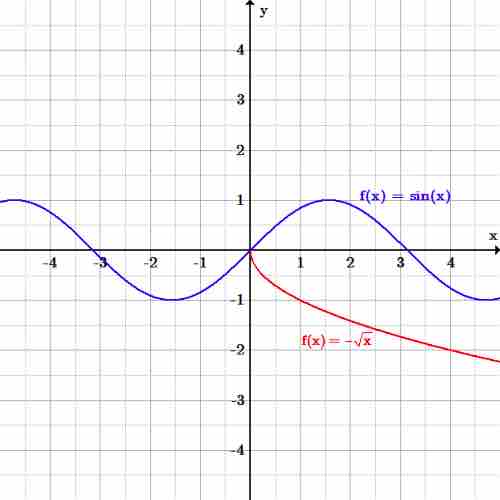
Domain and range graph

The blue graph is the trigonometric function $f(x)=sin (x)$ with a domain of $\mathbb{R}$ and a restricted range of $-1 \leq y \leq 1$ (output values only exist between $-1$ to $1$.  The red graph is the function $f(x)=-\sqrt{x}$ with a restricted domain of $x \geq 0$, and also a restricted range of $y\leq0$.