Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Combinatorial techniques are applicable to many areas of mathematics, and a knowledge of combinatorics is necessary to build a solid command of statistics. It involves the enumeration, combination, and permutation of sets of elements and the mathematical relations that characterize their properties.
Aspects of combinatorics include: counting the structures of a given kind and size, deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria. Aspects also include finding "largest," "smallest," or "optimal" objects, studying combinatorial structures arising in an algebraic context, or applying algebraic techniques to combinatorial problems.
Combinatorial Rules and Techniques
Several useful combinatorial rules or combinatorial principles are commonly recognized and used. Each of these principles is used for a specific purpose. The rule of sum (addition rule), rule of product (multiplication rule), and inclusion-exclusion principle are often used for enumerative purposes. Bijective proofs are utilized to demonstrate that two sets have the same number of elements. Double counting is a method of showing that two expressions are equal. The pigeonhole principle often ascertains the existence of something or is used to determine the minimum or maximum number of something in a discrete context. Generating functions and recurrence relations are powerful tools that can be used to manipulate sequences, and can describe if not resolve many combinatorial situations. Each of these techniques is described in greater detail below.
Rule of Sum
The rule of sum is an intuitive principle stating that if there are
Rule of Product
The rule of product is another intuitive principle stating that if there are
Inclusion-Exclusion Principle
The inclusion-exclusion principle is a counting technique that is used to obtain the number of elements in a union of multiple sets. This counting method ensures that elements that are present in more than one set in the union are not counted more than once. It considers the size of each set and the size of the intersections of the sets. The smallest example is when there are two sets: the number of elements in the union of
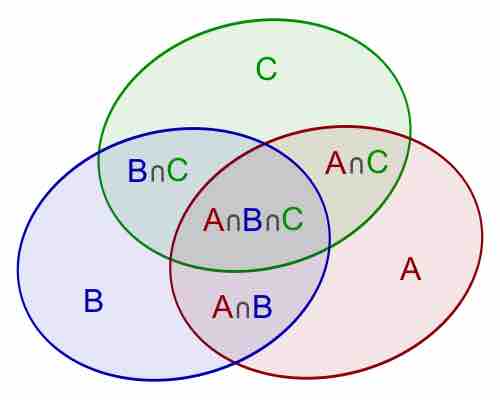
Inclusion-Exclusion Principle
Inclusion–exclusion illustrated for three sets
Bijective Proof
A bijective proof is a proof technique that finds a bijective function
Double Counting
Double counting is a combinatorial proof technique for showing that two expressions are equal. This is done by demonstrating that the two expressions are two different ways of counting the size of one set. In this technique, a finite set
Pigeonhole Principle
The pigeonhole principle states that if
Generating Function
Generating functions can be thought of as polynomials with infinitely many terms whose coefficients correspond to the terms of a sequence. The (ordinary) generating function of a sequence
whose coefficients give the sequence
Recurrence Relation
A recurrence relation defines each term of a sequence in terms of the preceding terms. In other words, once one or more initial terms are given, each of the following terms of the sequence is a function of the preceding terms.
The Fibonacci sequence is one example of a recurrence relation. Each term of the Fibonacci sequence is given by