ANOVA Design

There are several types of ANOVA. Many statisticians base ANOVA on the design of the experiment, especially on the protocol that specifies the random assignment of treatments to subjects. The protocol's description of the assignment mechanism should include a specification of the structure of the treatments and of any blocking. It is also common to apply ANOVA to observational data using an appropriate statistical model. Some popular designs use the following types of ANOVA.

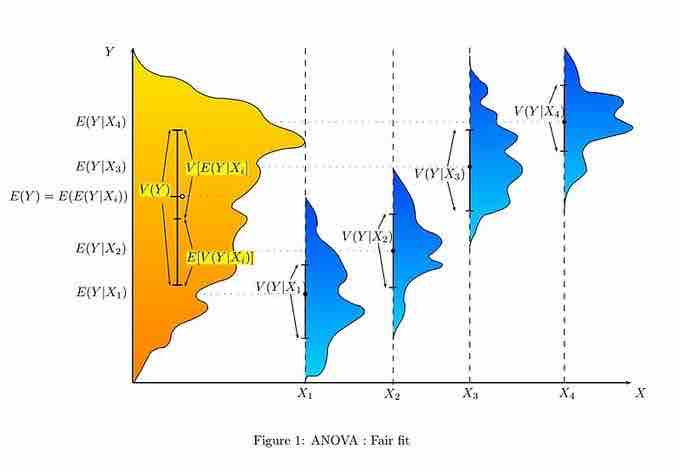
ANOVA With Fair Fit

This graph shows a representation of a situation with a fair fit in terms of ANOVA statistics.

1. One-way ANOVA is used to test for differences among two or more independent groups. Typically, however, the one-way ANOVA is used to test for differences among at least three groups, since the two-group case can be covered by a $t$-test. When there are only two means to compare, the $t$-test and the ANOVA $F$-test are equivalent.
2. Factorial ANOVA is used when the experimenter wants to study the interaction effects among the treatments.
3. Repeated measures ANOVA is used when the same subjects are used for each treatment (e.g., in a longitudinal study).
4. Multivariate analysis of variance (MANOVA) is used when there is more than one response variable.

ANOVA for a Single Factor

The simplest experiment suitable for ANOVA analysis is the completely randomized experiment with a single factor. More complex experiments with a single factor involve constraints on randomization and include completely randomized blocks. The more complex experiments share many of the complexities of multiple factors.

ANOVA for Multiple Factors

ANOVA generalizes to the study of the effects of multiple factors. When the experiment includes observations at all combinations of levels of each factor, it is termed factorial. Factorial experiments are more efficient than a series of single factor experiments, and the efficiency grows as the number of factors increases. Consequently, factorial designs are heavily used.

The use of ANOVA to study the effects of multiple factors has a complication. In a 3-way ANOVA with factors $x$, $y$, and $z$, the ANOVA model includes terms for the main effects ($x$, $y$, $z$) and terms for interactions ($xy$, $xz$, $yz$, $xyz$). All terms require hypothesis tests. The proliferation of interaction terms increases the risk that some hypothesis test will produce a false positive by chance. Fortunately, experience says that high order interactions are rare. The ability to detect interactions is a major advantage of multiple factor ANOVA. Testing one factor at a time hides interactions, but produces apparently inconsistent experimental results.

Classes of Models

There are three classes of models used in the analysis of variance, and these are outlined here.

Fixed-Effects Models

The fixed-effects model of analysis of variance applies to situations in which the experimenter applies one or more treatments to the subjects of the experiment to see if the response variable values change. This allows the experimenter to estimate the ranges of response variable values that the treatment would generate in the population as a whole.

Random-Effects Models

Random effects models are used when the treatments are not fixed. This occurs when the various factor levels are sampled from a larger population. Because the levels themselves are random variables, some assumptions and the method of contrasting the treatments (a multi-variable generalization of simple differences) differ from the fixed-effects model.

Mixed-Effects Models

A mixed-effects model contains experimental factors of both fixed and random-effects types, with appropriately different interpretations and analysis for the two types. For example, teaching experiments could be performed by a university department to find a good introductory textbook, with each text considered a treatment. The fixed-effects model would compare a list of candidate texts. The random-effects model would determine whether important differences exist among a list of randomly selected texts. The mixed-effects model would compare the (fixed) incumbent texts to randomly selected alternatives.