A full factorial experiment is an experiment whose design consists of two or more factors, each with discrete possible values (or levels), and whose experimental units take on all possible combinations of these levels across all such factors. A full factorial design may also be called a fully crossed design. Such an experiment allows the investigator to study the effect of each factor on the response variable, as well as the effects of interactions between factors on the response variable.
For the vast majority of factorial experiments, each factor has only two levels. For example, with two factors each taking two levels, a factorial experiment would have four treatment combinations in total, and is usually called a 2 by 2 factorial design.
If the number of combinations in a full factorial design is too high to be logistically feasible, a fractional factorial design may be done, in which some of the possible combinations (usually at least half) are omitted.
Notation
To save space, the points in a two-level factorial experiment are often abbreviated with strings of plus and minus signs. The strings have as many symbols as factors, and their values dictate the level of each factor: conventionally,

Factorial Notation
This table shows the notation used for a 2x2 factorial experiment.
The factorial points can also be abbreviated by (1),
Analysis
A factorial experiment can be analyzed using ANOVA or regression analysis. It is relatively easy to estimate the main effect for a factor. To compute the main effect of a factor
Other useful exploratory analysis tools for factorial experiments include main effects plots, interaction plots, and a normal probability plot of the estimated effects.
When the factors are continuous, two-level factorial designs assume that the effects are linear. If a quadratic effect is expected for a factor, a more complicated experiment should be used, such as a central composite design.
Example
The simplest factorial experiment contains two levels for each of two factors. Suppose an engineer wishes to study the total power used by each of two different motors,
This experiment is an example of a
Designs can involve many independent variables. As a further example, the effects of three input variables can be evaluated in eight experimental conditions shown as the corners of a cube.
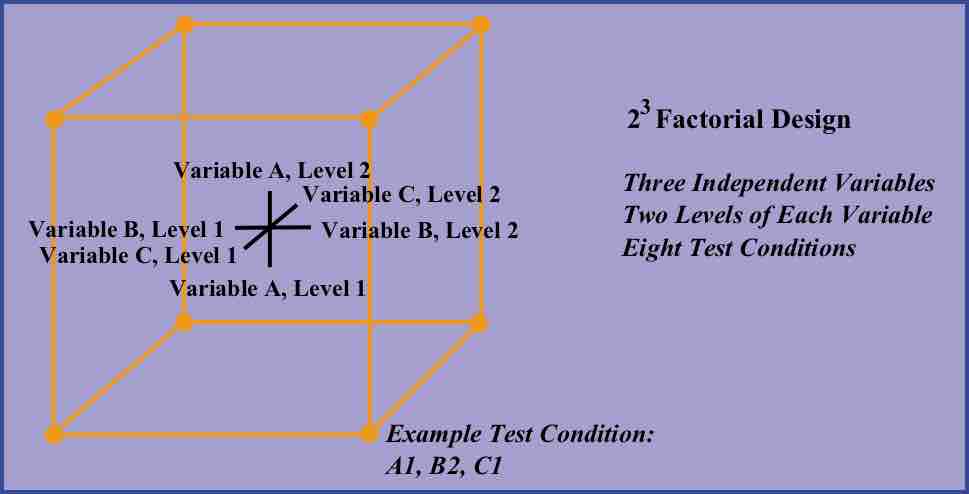
Factorial Design
This figure is a sketch of a 2 by 3 factorial design.
This can be conducted with or without replication, depending on its intended purpose and available resources. It will provide the effects of the three independent variables on the dependent variable and possible interactions.