The Root-Mean-Square

The root-mean-square, also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity, or set of numbers. It can be calculated for a series of discrete values or for a continuously varying function. Its name comes from its definition as the square root of the mean of the squares of the values.

This measure is especially useful when a data set includes both positive and negative numbers. For example, consider the set of numbers $[-2, 5, -8, 9, -4]$. Computing the average of this set of numbers wouldn't tell us much because the negative numbers cancel out the positive numbers, resulting in an average of zero. This gives us the "middle value" but not a sense of the average magnitude.

One possible method of assigning an average to this set would be to simply erase all of the negative signs. This would lead us to compute an average of 5.6. However, using the RMS method, we would square every number (making them all positive) and take the square root of the average. Explicitly, the process is to:

1. Square all of the values
2. Compute the average of the squares
3. Take the square root of the average

In our example:

1. $(-2)^2+5^2 +(-8)^2 + 9^2+(-4)^2$
2. $\displaystyle \frac{4+25+64+81+16}{5} = 38$
3. $\sqrt{38} \approx 6.16$

The root-mean-square is always greater than or equal to the average of the unsigned values. Physical scientists often use the term "root-mean-square" as a synonym for standard deviation when referring to the square root of the mean squared deviation of a signal from a given baseline or fit. This is useful for electrical engineers in calculating the "AC only" RMS of an electrical signal. Standard deviation being the root-mean-square of a signal's variation about the mean, rather than about 0, the DC component is removed (i.e. the RMS of the signal is the same as the standard deviation of the signal if the mean signal is zero).

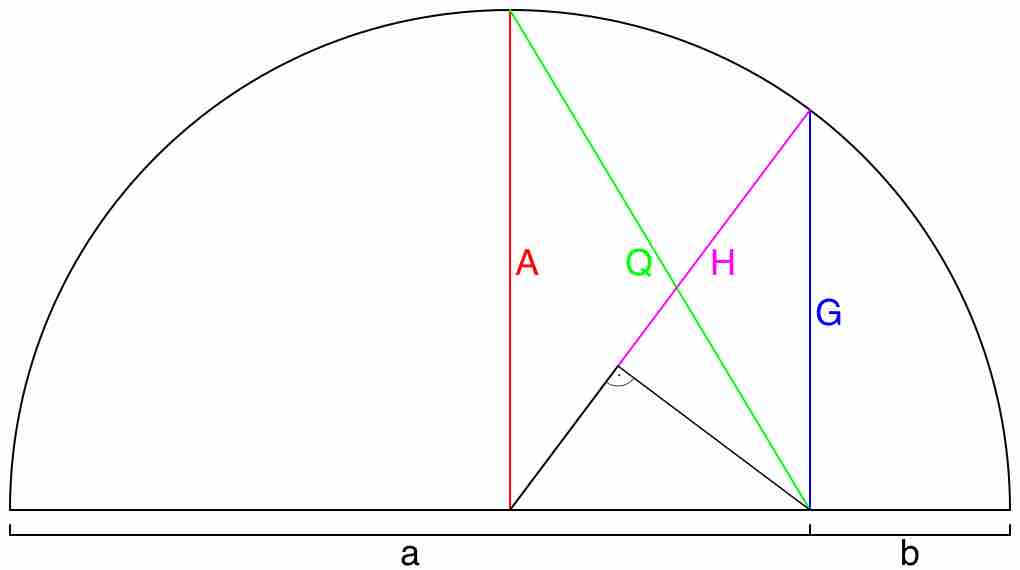
Mathematical Means

This is a geometrical representation of common mathematical means. $a$, $b$ are scalars. $A$ is the arithmetic mean of scalars $a$ and $b$. $G$ is the geometric mean, $H$ is the harmonic mean, $Q$ is the quadratic mean (also known as root-mean-square).