A continuous probability distribution is a probability distribution that has a probability density function. Mathematicians also call such a distribution "absolutely continuous," since its cumulative distribution function is absolutely continuous with respect to the Lebesgue measure
Intuitively, a continuous random variable is the one which can take a continuous range of values—as opposed to a discrete distribution, in which the set of possible values for the random variable is at most countable. While for a discrete distribution an event with probability zero is impossible (e.g. rolling 3 and a half on a standard die is impossible, and has probability zero), this is not so in the case of a continuous random variable.
For example, if one measures the width of an oak leaf, the result of 3.5 cm is possible; however, it has probability zero because there are uncountably many other potential values even between 3 cm and 4 cm. Each of these individual outcomes has probability zero, yet the probability that the outcome will fall into the interval (3 cm, 4 cm) is nonzero. This apparent paradox is resolved given that the probability that
The definition states that a continuous probability distribution must possess a density; or equivalently, its cumulative distribution function be absolutely continuous. This requirement is stronger than simple continuity of the cumulative distribution function, and there is a special class of distributions—singular distributions, which are neither continuous nor discrete nor a mixture of those. An example is given by the Cantor distribution. Such singular distributions, however, are never encountered in practice.
Probability Density Functions
In theory, a probability density function is a function that describes the relative likelihood for a random variable to take on a given value. The probability for the random variable to fall within a particular region is given by the integral of this variable's density over the region. The probability density function is nonnegative everywhere, and its integral over the entire space is equal to one.
Unlike a probability, a probability density function can take on values greater than one. For example, the uniform distribution on the interval
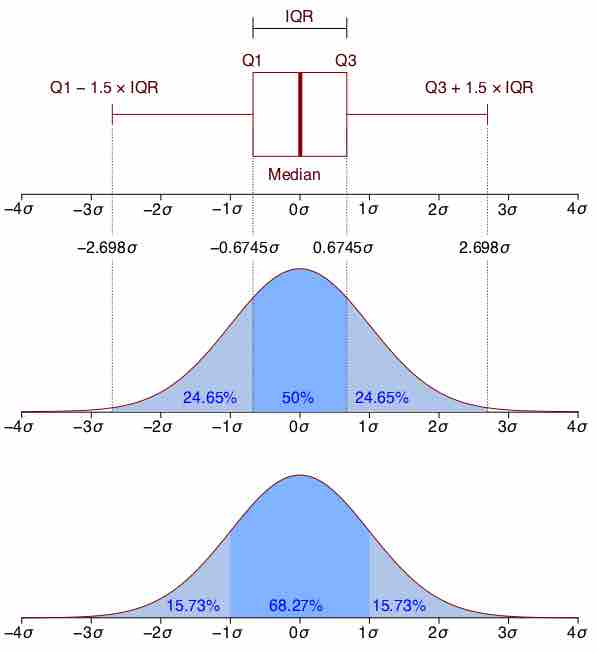
Boxplot Versus Probability Density Function
Boxplot and probability density function of a normal distribution