The potential difference in a resting neuron is called the resting membrane potential. This causes the membrane to be polarized. The value of the resting membrane potential varies from -40mV to -90mV in a different types of neurons.
The resting membrane potential exists only across the membrane. Most of the time, the difference in ionic composition of the intracellular and extracellular fluids and difference in ion permeability generates the resting membrane potential difference.
The interactions that generate the resting potential are modeled by the Goldman equation. It is based on the charges of the ions in question, as well as the difference between their inside and outside concentrations and the relative permeability of the plasma membrane to each ion where:
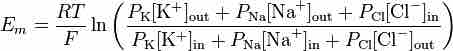
Goldman equation
Goldman equation: R is the universal gas constant, equal to 8.314 joules·K−1·mol−1 T is the absolute temperature, measured in kelvins (= K = degrees Celsius + 273.15) F is the Faraday constant, equal to 96,485 coulombs·mol−1 or J·V−1·mol−1
R is the universal gas constant, equal to 8.314 joules·K−1·mol−1. T is the absolute temperature measured in kelvins (= K = degrees Celsius + 273.15). F is the Faraday constant, equal to 96,485 coulombs·mol−1 or J·V−1·mol−1 .
The three ions that appear in this equation are potassium (K+), sodium (Na+), and chloride (Cl−). The Goldman formula essentially expresses the membrane potential as an average of the reversal potentials for the individual ion types, weighted by permeability. In most animal cells, the permeability to potassium is much higher in the resting state than the permeability to sodium. Consequently, the resting potential is usually close to the potassium reversal potential.