Conservation of Mechanical Energy

Conservation of mechanical energy states that the mechanical energy of an isolated system remains constant in time, as long as the system is free of all frictional forces. In any real situation, frictional forces and other non-conservative forces are always present, but in many cases their effects on the system are so small that the principle of conservation of mechanical energy can be used as a fair approximation. An example of a such a system is shown in . Though energy cannot be created nor destroyed in an isolated system, it can be internally converted to any other form of energy.

A Mechanical System

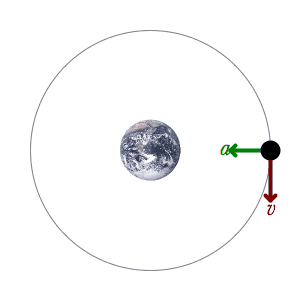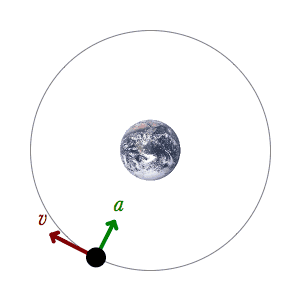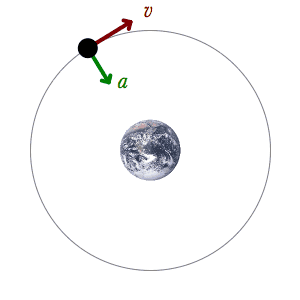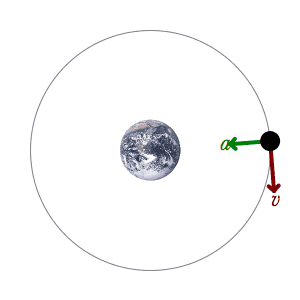
An example of a mechanical system: A satellite is orbiting the Earth only influenced by the conservative gravitational force and the mechanical energy is therefore conserved. This acceleration is represented by a green acceleration vector and the velocity is represented by a red velocity vector.

Derivation

Let us consider what form the work-energy theorem takes when only conservative forces are involved (leading us to the conservation of energy principle). The work-energy theorem states that the net work done by all forces acting on a system equals its change in kinetic energy (KE). In equation form, this is:

$W_{net} = \frac{1}{2} mv^2 - \frac{1}{2} m v_0^2 = \Delta KE$ .

If only conservative forces act, then W_net=W_c, where W_c is the total work done by all conservative forces. Thus, W_c = ΔKE. ,

Now, if the conservative force, such as the gravitational force or a spring force, does work, the system loses potential energy (PE). That is, W_c = −PE. Therefore,

$-\Delta PE = \Delta KE$.

This equation means that the total kinetic and potential energy is constant for any process involving only conservative forces. That is,

$KE + PE = const$ or $KE_i + PE_i = KE_f + PE_f$,

where i and f denote initial and final values. This equation is a form of the work-energy theorem for conservative forces; it is known as the conservation of mechanical energy principle.

Remember that the law applies to the extent that all the forces are conservative, so that friction is negligible. The total kinetic plus potential energy of a system is defined to be its mechanical energy (KE+PE). In a system that experiences only conservative forces, there is a potential energy associated with each force, and the energy only changes form between KE and various types of PE (with the total energy remaining constant).