Mathematical Represenation of a Traveling Wave

In general, one dimensional waves satisfy the 1D wave equation:

$\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}$.

For example, a sinusoidal form

$u(x,t) = A~ sin(kx-\omega t)$

is a solution of the wave equation for $c= \frac{\omega}{k}$. In this atom, we will obtain a general mathematical form of a traveling wave.

Solving the Wave Equation

First, we notice that any function u(x,t) satisfying

$\frac{\partial u}{\partial t} = \pm c \frac{\partial u}{\partial x}$ (Eq. 1)

is a solution to the wave equation. To show this, note that

$\begin{aligned} \frac{\partial ^2 u}{\partial t^2} &= \frac{\partial }{\partial t}(\frac{\partial u} {\partial t}) = \pm c \frac{\partial }{\partial t}( \frac{\partial u}{\partial x}) \\ &= \pm c \frac{\partial }{\partial x}( \frac{\partial u}{\partial t}) = c^2 \frac{\partial ^2 u}{\partial x^2} \end{aligned}$.

In the middle, we used the equation 1 along with the fact that partial derivatives are interchangeable.

To solve the equation 1, let's introduce new variables: $\phi = x-ct, \psi= x+ct$. From the chain rules,

$\frac{\partial }{\partial t} = \frac{\partial \phi}{\partial t} \frac{\partial}{\partial \phi} + \frac{\partial \psi}{\partial t} \frac{\partial}{\partial \psi} = -c \frac{\partial}{\partial \phi} + c \frac{\partial}{\partial \psi}$.

$\frac{\partial }{\partial x} = \frac{\partial \phi}{\partial x} \frac{\partial}{\partial \phi} + \frac{\partial \psi}{\partial x} \frac{\partial}{\partial \psi} = \frac{\partial}{\partial \phi} + \frac{\partial}{\partial \psi}$

With the change of variables, the equation 1 becomes $\frac{\partial u_+}{\partial \phi} = 0$ for the equation with the "+" sign and $\frac{\partial u_-}{\partial \psi} = 0$ for the "-" sign. Therefore, we see that

$u_+(\phi, \psi) = f(\psi), u_-(\phi, \psi) = g(\phi)$,

where f and g are arbitrary functions. Converting back to the original variables of x and t, we conclude that the solution of the original wave equation is

$u(x,t) = f(x+ct)+g(x-ct)$.

f(x+ct) represents a left-going traveling wave, while g(x-ct) represents a right-going traveling wave. In other words, solutions of the 1D wave equation are sums of a left traveling function f and a right traveling function g. "Traveling" means that the shape of these individual arbitrary functions with respect to x stays constant, however the functions are translated left and right with time at the speed c. This solution was derived by Jean le Rond d'Alembert.

Boundary Condition

Any function that contains "x+ct" or "x-ct" can be a solution of the wave equation. The wave function is further determined by taking additional information, usually given as boundary conditions and some others. For example, in the case of a string in a guitar, we know that the wave has zero amplitude at both ends: u(x=0)=u(x=L)=0 . Also, the shape of the function at an instance can be provided to determine the function.

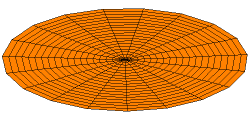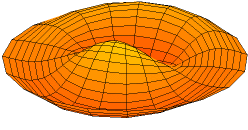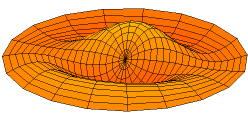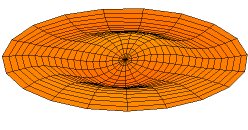
Wave Equation in Two Dimensions

A solution of the wave equation in two dimensions with a zero-displacement boundary condition along the entire outer edge.