The Simple Pendulum

The Simple Pendulum

A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting equilibrium position, it is subject to a restoring force; after it reaches its highest point in its swing, gravity will accelerate it back toward the equilibrium position. When released, the restoring force combined with the pendulum's mass causes it to oscillate about the equilibrium position, swinging back and forth .

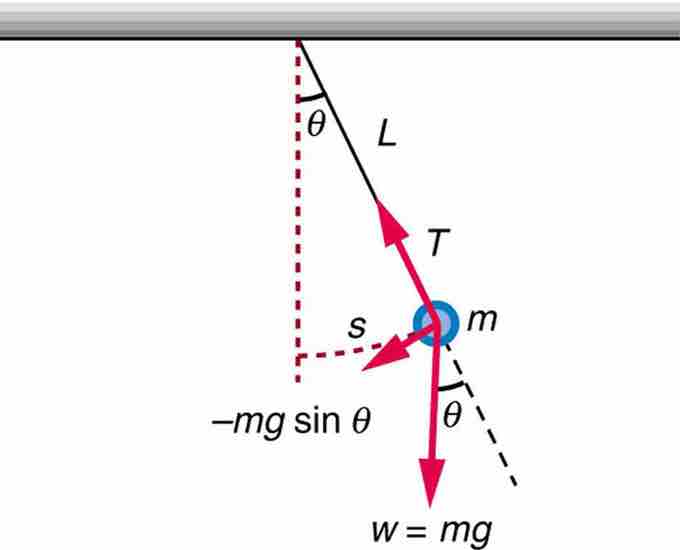
Simple Pendulum

A simple pendulum has a small-diameter bob and a string that has a very small mass but is strong enough not to stretch appreciably. The linear displacement from equilibrium is s, the length of the arc. Also shown are the forces on the bob, which result in a net force of −mgsinθ toward the equilibrium position—that is, a restoring force.

For small displacements, a pendulum is a simple harmonic oscillator. A simple pendulum is defined to have an object that has a small mass, also known as the pendulum bob, which is suspended from a wire or string of negligible mass, such as shown in the illustrating figure. Exploring the simple pendulum a bit further, we can discover the conditions under which it performs simple harmonic motion, and we can derive an interesting expression for its period.

We begin by defining the displacement to be the arc length s. We see from the figure that the net force on the bob is tangent to the arc and equals −mgsinθ. (The weight mg has components mgcosθ along the string and mgsinθ tangent to the arc. ) Tension in the string exactly cancels the component mgcosθ parallel to the string. This leaves a net restoring force drawing the pendulum back toward the equilibrium position at θ = 0.

Now, if we can show that the restoring force is directly proportional to the displacement, then we have a simple harmonic oscillator. In trying to determine if we have a simple harmonic oscillator, we should note that for small angles (less than about 15º), sinθ≈θ (sinθ and θ differ by about 1% or less at smaller angles). Thus, for angles less than about 15º, the restoring force F is

$F\approx -mg\theta$.

The displacement s is directly proportional to θ. When θ is expressed in radians, the arc length in a circle is related to its radius (L in this instance) by:

$s=L\theta$

so that

$\theta=\frac{s}{L}$.

For small angles, then, the expression for the restoring force is:

$F\approx \frac{mgL}{s}$.

This expression is of the form of Hooke's Law:

$F\approx -kx$

where the force constant is given by k=mg/L and the displacement is given by x=s. For angles less than about 15º, the restoring force is directly proportional to the displacement, and the simple pendulum is a simple harmonic oscillator.

Using this equation, we can find the period of a pendulum for amplitudes less than about 15º. For the simple pendulum:

$T=2\pi \sqrt{\frac{m}{k}}=2\pi\sqrt{\frac{m}{\frac{mg}{L}}}$.

Thus,

$T=2\pi \sqrt{\frac{L}{g}}$

or the period of a simple pendulum. This result is interesting because of its simplicity. The only things that affect the period of a simple pendulum are its length and the acceleration due to gravity. The period is completely independent of other factors, such as mass. Even simple pendulum clocks can be finely adjusted and accurate. Note the dependence of T on g. If the length of a pendulum is precisely known, it can actually be used to measure the acceleration due to gravity. If θ is less than about 15º, the period T for a pendulum is nearly independent of amplitude, as with simple harmonic oscillators. In this case, the motion of a pendulum as a function of time can be modeled as:

$\theta (t)=\theta _{o}cos(\frac{2\pi t}{T})$

For amplitudes larger than 15º, the period increases gradually with amplitude so it is longer than given by the simple equation for T above. For example, at an amplitude of θ₀ = 23° it is 1% larger. The period increases asymptotically (to infinity) as θ₀ approaches 180°, because the value θ₀ = 180° is an unstable equilibrium point for the pendulum.