The Physical Pendulum

The Physical Pendulum

Recall that a simple pendulum consists of a mass suspended from a massless string or rod on a frictionless pivot. In that case, we are able to neglect any effect from the string or rod itself. In contrast, a physical pendulum (sometimes called a compound pendulum) may be suspended by a rod that is not massless or, more generally, may be an arbitrarily-shaped, rigid body swinging by a pivot (see ). In this case, the pendulum's period depends on its moment of inertia around the pivot point .

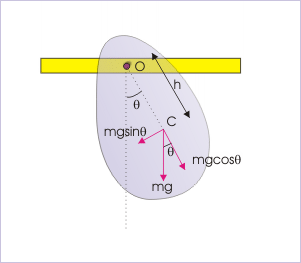
A Physical Pendulum

An example showing how forces act through center of mass. We can calculate the period of this pendulum by determining the moment of inertia of the object around the pivot point.

Gravity acts through the center of mass of the rigid body. Hence, the length of the pendulum used in equations is equal to the linear distance between the pivot and the center of mass (h).

The equation of torque gives:

$\tau=I\alpha$,

where α is the angular acceleration, τ is the torque, and I is the moment of inertia.

The torque is generated by gravity so:

$\tau=mghsin\theta$,

where h is the distance from the center of mass to the pivot point and θ is the angle from the vertical.

Hence, under the small-angle approximation sin\theta \approx \theta,

$\alpha\approx -\frac{mgh\theta }{I}$.

This is of the same form as the conventional simple pendulum and this gives a period of:

$T=2\pi \sqrt{\frac{I}{mgh}}$.

And a frequency of:

$f=\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{mgh}{I}}$.

In case we know the moment of inertia of the rigid body, we can evaluate the above expression of the period for the physical pendulum. For illustration, let us consider a uniform rigid rod, pivoted from a frame as shown (see ). Clearly, the center of mass is at a distance L/2 from the point of suspension:

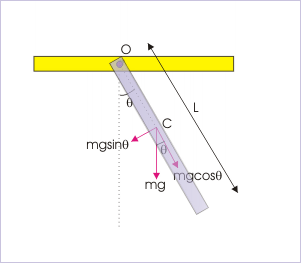
Uniform Rigid Rod

A rigid rod with uniform mass distribution hangs from a pivot point. This is another example of a physical pendulum.

$h=\frac{L}{2}$.

The moment of inertia of the rigid rod about its center is:

$I_{c}=\frac{mL^{2}}{12}$.

However, we need to evaluate the moment of inertia about the pivot point, not the center of mass, so we apply the parallel axis theorem:

$I_{o}=I_{c}+mh^{2}=\frac{mL^{2}}{12}+m(\frac{L}{2})^{2}=\frac{mL^{2}}{3}$.

Plugging this result into the equation for period, we have:

$T=2\pi \sqrt{\frac{I}{mgh}}=2\pi\sqrt{\frac{2mL^{2}}{3mgL}}=2\pi\sqrt{\frac{2L}{3g}}$.

The important thing to note about this relation is that the period is still independent of the mass of the rigid body. However, it is not independent of the mass distribution of the rigid body. A change in shape, size, or mass distribution will change the moment of inertia. This, in turn, will change the period.

As with a simple pendulum, a physical pendulum can be used to measure g.