Sinusoidal Nature of Simple Harmonic Motion

Sinusoidal Nature of Simple Harmonic Motion

Why are sine waves so common?

If the mass-on-a-spring system discussed in previous sections were to be constructed and its motion were measured accurately, its x-t graph would be a near-perfect sine-wave shape, as shown in . It is called a "sine wave" or "sinusoidal" even if it is a cosine, or a sine or cosine shifted by some arbitrary horizontal amount. It may not be surprising that it is a wiggle of this general sort, but why is it a specific mathematically perfect shape? Why is it not a sawtooth shape, like in (2); or some other shape, like in (3)? It is notable that a vast number of apparently unrelated vibrating systems show the same mathematical feature. A tuning fork, a sapling pulled to one side and released, a car bouncing on its shock absorbers, all these systems will exhibit sine-wave motion under one condition: the amplitude of the motion must be small.

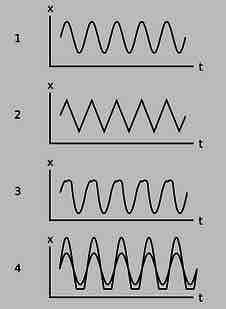
Sinusoidal and Non-Sinusoidal Vibrations

Only the top graph is sinusoidal. The others vary with constant amplitude and period, but do no describe simple harmonic motion.

Hooke's Law and Sine Wave Generation

The key to understanding how an object vibrates is to know how the force on the object depends on the object's position. If a system follows Hooke's Law, the restoring force is proportional to the displacement. As touched on in previous sections, there exists a second order differential equation that relates acceleration and displacement.

$F_{net}=m\frac{d^{2}x}{dt^{2}}=-kx$.

When this general equation is solved for the position, velocity and acceleration as a function of time:

• $x(t)=Acos(\omega t-\varphi )$
• $v(t)=\frac{dx}{dt}=-A\omega sin(\omega t-\varphi )$
• $a(t)=\frac{d^{2}x}{dt^{2}}=-A\omega^{2} cos(\omega t-\varphi )$

These are all sinusoidal solutions . Consider a mass on a spring that has a small pen inside running across a moving strip of paper as it bounces, recording its movements.

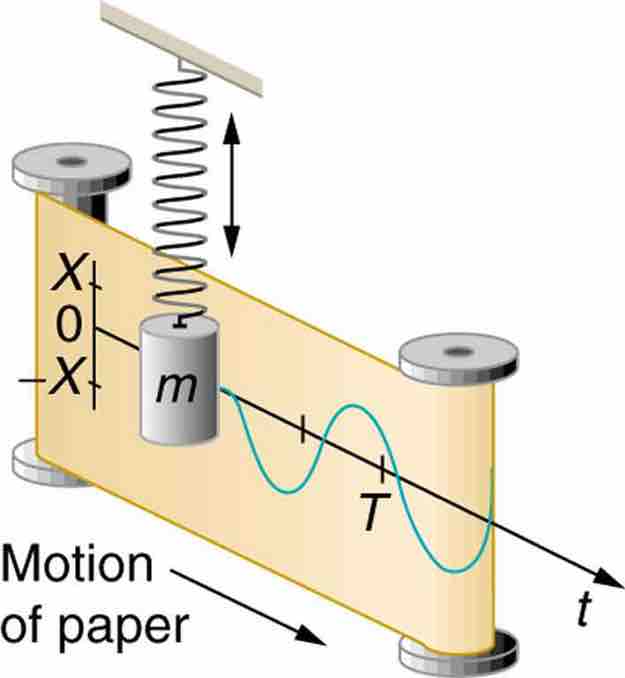
Mass on Spring Producing Sine Wave

The vertical position of an object bouncing on a spring is recorded on a strip of moving paper, leaving a sine wave.

The above equations can be rewritten in a form applicable to the variables for the mass on spring system in the figure.

• $x(t)=Xcos(\frac{2\pi t}{T})$
• $v(t)=-v_{max}sin(\frac{2\pi t}{T})$
• $a(t)=-\frac{kX}{m}cos(\frac{2\pi t}{T})$

Recall that the projection of uniform circular motion can be described in terms of a simple harmonic oscillator. Uniform circular motion is therefore also sinusoidal, as you can see from .

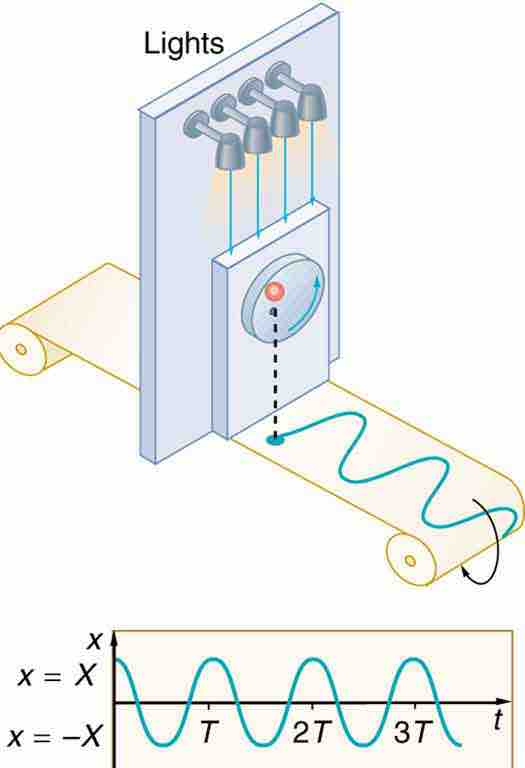
Sinusoidal Nature of Uniform Circular Motion

The position of the projection of uniform circular motion performs simple harmonic motion, as this wavelike graph of x versus t indicates.

Instantaneous Energy of Simple Harmonic Motion

The equations discussed for the components of the total energy of simple harmonic oscillators may be combined with the sinusoidal solutions for x(t), v(t), and a(t) to model the changes in kinetic and potential energy in simple harmonic motion.

The kinetic energy K of the system at time t is:

$K(t)=\frac{1}{2}mv^{2}(t)=\frac{1}{2}m\omega ^{2}A^{2}sin^{2}(\omega t-\varphi )=\frac{1}{2}kA^{2}sin^{2}(\omega t-\varphi )$.

The potential energy U is:

$U(t)=\frac{1}{2}kx^{2}(t)==\frac{1}{2}kA^{2}cos^{2}(\omega t-\varphi )$.

Summing K(t) and U(t) produces the total mechanical energy seen before:

$E=K+U=\frac{1}{2}kA^{2}$.