Driven Oscillations and Resonance

In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: $\vec F = -k \vec x$ where k is a positive constant. If a frictional force (damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator.

Driven harmonic oscillators are damped oscillators further affected by an externally applied force F(t). Newton's second law takes the form $F(t)-kx-c\frac{\mathrm{d}x}{\mathrm{d}t}=m\frac{\mathrm{d}^2x}{\mathrm{d}t^2}$. It is usually rewritten into the form $\frac{\mathrm{d}^2x}{\mathrm{d}t^2} + 2\zeta\omega_0\frac{\mathrm{d}x}{\mathrm{d}t} + \omega_0^2 x = \frac{F(t)}{m}$. This equation can be solved exactly for any driving force, using the solutions z(t) which satisfy the unforced equation: $\frac{\mathrm{d}^2z}{\mathrm{d}t^2} + 2\zeta\omega_0\frac{\mathrm{d}z}{\mathrm{d}t} + \omega_0^2 z = 0$, and which can be expressed as damped sinusoidal oscillations $z(t) = A \mathrm{e}^{-\zeta \omega_0 t} \ \sin \left( \sqrt{1-\zeta^2} \ \omega_0 t + \varphi \right)$in the case where ζ ≤ 1. The amplitude A and phase φ determine the behavior needed to match the initial conditions. In the case ζ < 1 and a unit step input with x(0) = 0 the solution is: $x(t) = 1 - \mathrm{e}^{-\zeta \omega_0 t} \frac{\sin \left( \sqrt{1-\zeta^2} \ \omega_0 t + \varphi \right)}{\sin(\varphi)}$with phase φ given by $\cos \varphi = \zeta$. The time an oscillator needs to adapt to changed external conditions is of the order τ = 1/(ζ₀). In physics, the adaptation is called relaxation, and τ is called the relaxation time.

In the case of a sinusoidal driving force: $\frac{\mathrm{d}^2x}{\mathrm{d}t^2} + 2\zeta\omega_0\frac{\mathrm{d}x}{\mathrm{d}t} + \omega_0^2 x = \frac{1}{m} F_0 \sin(\omega t)$, where $\!F_0$ is the driving amplitude and $\!\omega$ is the driving frequency for a sinusoidal driving mechanism. This type of system appears in AC driven RLC circuits (resistor-inductor-capacitor) and driven spring systems having internal mechanical resistance or external air resistance. The general solution is a sum of a transient solution that depends on initial conditions, and a steady state that is independent of initial conditions and depends only on the driving amplitude $\!F_0$, driving frequency $\!\omega$, undamped angular frequency $\!\omega_0$, and the damping ratio $\!\zeta$. For a particular driving frequency called the resonance, or resonant frequency $\!\omega_r = \omega_0\sqrt{1-2\zeta^2}$, the amplitude (for a given $\!F_0$) is maximum. This resonance effect only occurs when $\zeta < 1 / \sqrt{2}$, i.e. for significantly underdamped systems. For strongly underdamped systems the value of the amplitude can become quite large near the resonance frequency (see ).

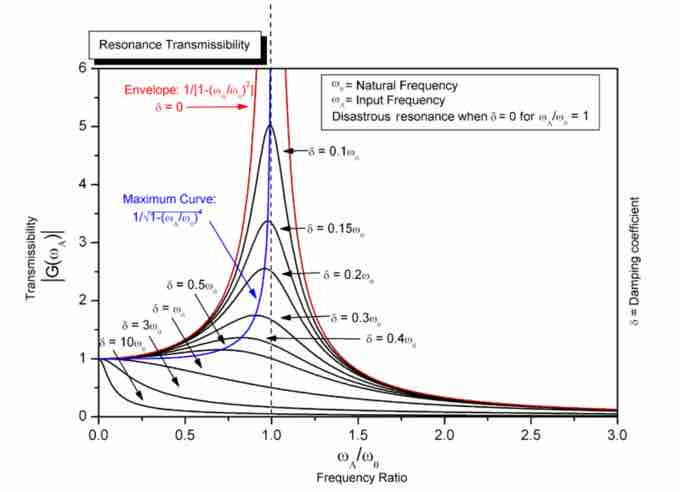
Resonance

Steady state variation of amplitude with frequency and damping of a driven simple harmonic oscillator.