Overview

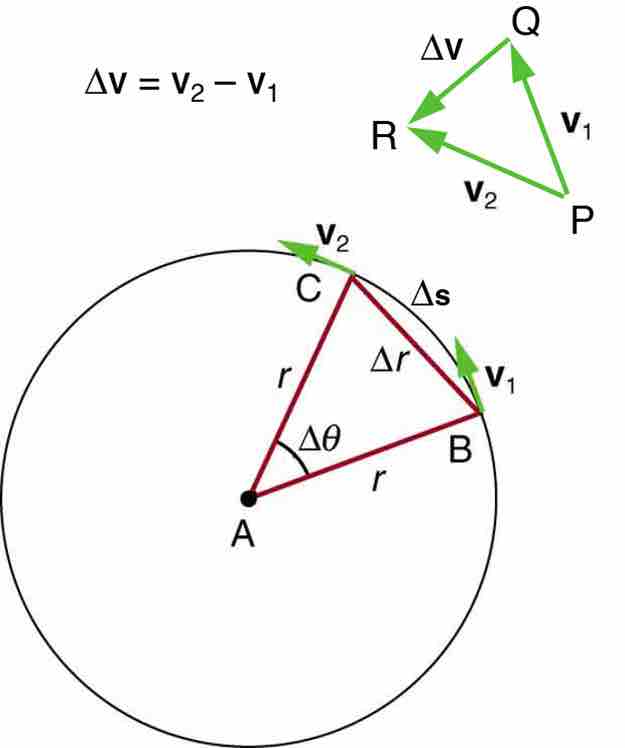
As mentioned in previous sections on kinematics, any change in velocity is given by an acceleration. Often the changes in velocity are changes in magnitude. When an object speeds up or slows down this is a change in the objects velocity. Changes in the magnitude of the velocity match our intuitive and every day usage of the term accelerate. However, because velocity is a vector, it also has a direction. Therefore, any change in the direction of travel of an object must also be met with an acceleration.

Uniform circular motion involves an object traveling a circular path at constant speed. Since the speed is constant, one would not usually think that the object is accelerating. However, the direction is constantly changing as the object traverses the circle. Thus, it is said to be accelerating. One can feel this acceleration when one is on a roller coaster. Even if the speed is constant, a quick turn will provoke a feeling of force on the rider. This feeling is an acceleration.

Calculating Centripetal Acceleration

To calculate the centripetal acceleration of an object undergoing uniform circular motion, it is necessary to have the speed at which the object is traveling and the radius of the circle about which the motion is taking place. The simple equation is:

$\displaystyle a_c = \frac{v^2}{r}$

where $v$ is the linear velocity of the object and $r$ is the radius of the circle.

The centripetal acceleration may also be expressed in terms of rotational velocity as follows:

$a_c = \omega^2 r$

with omega being the rotational velocity given by $\frac{v}{r}$.

Centripetal Acceleration

As an object moves around a circle, the direction of the velocity vector constantly changes.