A force that causes motion in a curved path is called a centripetal force. Uniform circular motion is an example of centripetal force in action. It can be seen in the orbit of satellites around the earth, the tension in a rope in a game of tether ball, a roller coaster loop de loop, or in a bucket swung around the body.
Previously, we learned that any change in a velocity is an acceleration. As the object moves through the circular path it is constantly changing direction, and therefore accelerating—causing constant force to be acting on the object. This centripetal force acts toward the center of curvature, toward the axis of rotation. Because the object is moving perpendicular to the force, the path followed by the object is a circular one. It is this force that keeps a ball from falling out of a bucket if you swing it in circular continuously.
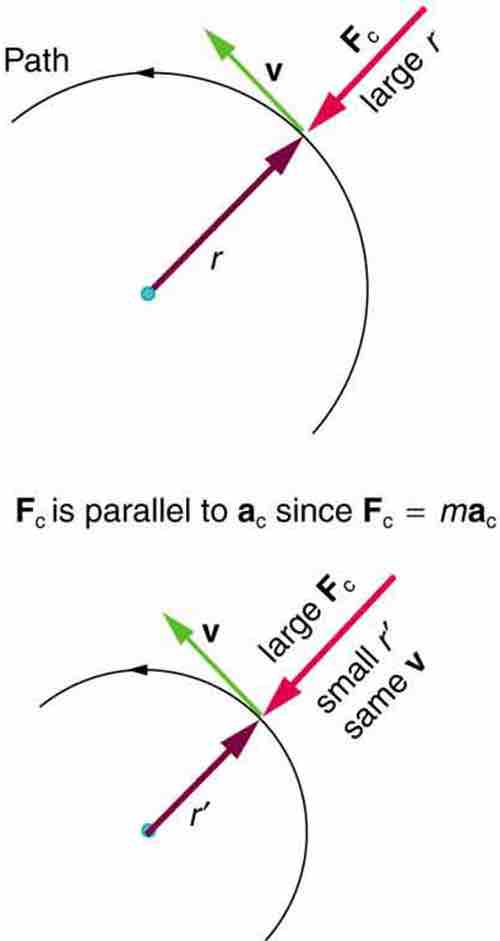
Centripetal force
As an object travels around a circular path at a constant speed, it experiences a centripetal force accelerating it toward the center.
The equation for centripetal force is as follows:
where:
From Newton's second law
Centripetal force can also be expressed in terms of angular velocity. Angular velocity is the measure of how fast an object is traversing the circular path. As the object travels its path, it sweeps out an arc that can be measured in degrees or radians. The equation for centripetal force using angular velocity is: